L’intérêt des algorithmes
Pour commencer, posons-nous la question de la pertinence de l’apprentissage des algorithmes, et examinons en détail les divers domaines abordés dans ce domaine d’étude.
Le domaine de l’informatique est rempli de termes à la mode tels que l’intelligence artificielle, l’apprentissage automatique, le cloud, l’informatique quantique, etc. Cependant, un terme en particulier est omniprésent dans le domaine de l’informatique, et c’est le mot « algorithme ».
De manière concrète, les algorithmes se résument à une séquence d’instructions suivies pas à pas dans le but d’accomplir une tâche utile ou de résoudre un problème donné. On pourrait assimiler une recette de cuisine à un exemple d’algorithme pour préparer un gâteau, par exemple.
Alors, pourquoi associons-nous systématiquement le terme « algorithme » à l’informatique, en particulier aux ordinateurs ? C’est simplement parce qu’un algorithme représente essentiellement un ensemble de méthodes utilisées par un ordinateur pour résoudre un problème. En réalité, vous réfléchissez d’abord à diverses approches pour résoudre un problème, puis vous demandez à l’ordinateur de le faire pour vous. Pourquoi ? Ce n’est pas simplement par paresse ! Les ordinateurs possèdent des capacités étendues que nous, en tant qu’êtres humains, ne pouvons pas égaler.
Tout d’abord, un ordinateur n’émettra pas de plainte si vous lui demandez d’effectuer des tâches répétitives. Au contraire ! Déplacer vos 2 000 dernières photos de voyage une par une ? C’est un jeu d’enfant pour lui. Rechercher dans ce document PDF de 200 pages toutes les occurrences de l’expression « max tout-puissant » ? C’est un jeu d’enfant. Imaginez si vous deviez accomplir ces tâches vous-même ! Le simple fait de transférer 2 000 photos d’un album papier à un autre vous ennuyerait à mourir…
Une autre raison, et elle n’est pas des moindres, c’est que l’ordinateur est bien plus rapide que nous. Il est plus efficace ! Essayez de calculer mentalement 10 x 20 x 30 x 40, puis comparez le temps que cela vous a pris avec celui d’un ordinateur. L’ordinateur est imbattable !
Analysons notre vie quotidienne en termes d’algorithme.
Nous utilisons des algorithmes au quotidien lorsque nous sommes confrontés à plusieurs options et que nous devons faire un choix. Prenons un exemple : vous prévoyez de rendre visite à votre grand-mère, mais il y a des travaux sur la route et vous devez modifier votre trajet habituel. De nos jours, la plupart d’entre nous auraient recours à leur GPS pour que l’ordinateur, notre ami, nous indique le chemin le plus rapide afin de déguster rapidement la tarte aux pommes qui doit déjà être sortie du four (après tout, certaines priorités dans la vie !).
Que feriez-vous sans un ordinateur ? Vous auriez probablement sorti une carte papier et planifié l’itinéraire optimal en prenant en compte divers paramètres : limites de vitesse sur chaque portion de route, frais de péage, votre emplacement actuel. Vous choisiriez ensuite l’itinéraire le plus rapide en tenant compte de tous ces facteurs.
Bravo, vous pourriez effectivement remplacer l’ordinateur ! Cependant, vous auriez probablement passé une bonne dizaine de minutes à réfléchir, laissant ainsi la tarte aux pommes refroidir, seule et abandonnée dans la cuisine de votre grand-mère.
Heureusement, des informaticiens ont élaboré un algorithme et l’ont mis en œuvre dans ce petit appareil fixé sur votre pare-brise !
Les algorithmes du quotidien
Pourquoi apprendre l’algorithmique ? Car ses concepts vous ouvrent des portes vers bien des domaines, allant de la recherche en ligne à la conception de jeux vidéo.
Le tri algorithmique des sites web
Vous avez certainement remarqué que Facebook adapte votre fil d’actualité en fonction de votre activité. Votre page d’accueil n’affiche pas les dernières publications de vos amis, mais bien ce que Facebook considère comme étant le contenu le plus pertinent pour vous, compte tenu de votre activité.
Vous souhaitez en savoir plus ? Découvrez le cours Lancez une campagne Facebook Ads dans lequel vous sera expliqué en détail le fonctionnement de cet algorithme.
De même, lorsque vous effectuez une recherche sur Google, vous vous attendez à ce que la page affiche les résultats les plus pertinents, et non les derniers sites parus sur le domaine. Google a donc besoin d’un modèle pour déterminer comment calculer la pertinence de ces résultats en prenant en compte plusieurs paramètres tels que votre historique de recherche, le nombre de visites sur un site, le nombre de liens pointant vers le site, etc.
Ces deux exemples utilisent des méthodes de machine learning (ou apprentissage automatique) extrêmement intéressantes.
Pour en savoir plus, je vous conseille cette excellente vidéo de David Louapre (Science étonnante), Découvrir le machine learning et le deep learning, et surtout l’excellent cours de Yannis Chaouche, Initiez-vous au Machine Learning.
Les algorithmes appliqués à la géolocalisation
Votre GPS intègre un algorithme qui lui permet de déterminer le plus court chemin entre votre position actuelle et celle que vous lui avez indiquée. De même, les nombreux sites de réservation en ligne intègrent un algorithme qui gère les places libres dans un train, mais également les correspondances et les problèmes éventuels (annulation, par exemple).
Les algorithmes sont également utilisés dans des logiciels de reconnaissance d’image ou par votre banque lorsque vous effectuez des paiements sur Internet (détection de fraude). C’est très puissant !
Nous pourrions trouver bien plus d’exemples d’algorithmes intégrés à notre vie quotidienne. Leur point commun : répondre à une problématique que nous nous posons par l’utilisation d’un programme.
Qu’est-ce qu’un programme ?
Un programme est un ensemble d’instructions exécutables par un ordinateur et qui permet à ce dernier de répondre à un problème que nous nous posons. Un programme est essentiellement créé à l’aide d’un ensemble d’algorithmes. Par exemple, imaginons que je souhaite écrire une nouvelle version du dernier box-office de l’année. Je peux bien sûr utiliser une feuille et un crayon, mais comment la partager avec des amis ? Que se passe-t-il si je renverse mon café dessus ? Si un ami perd le manuscrit ? Etc. Après avoir pleuré toutes les larmes de mon corps, et m’être juré de ne plus boire de café ni de fréquenter d’humains pendant le restant de mes jours, je vais certainement allumer mon ordinateur et utiliser Microsoft Word.
D’ailleurs, comment fonctionne un programme ? De manière assez simple : il prend un ensemble de données en entrée, exécute des instructions puis retourne des données en sortie.
Tiens, cela me rappelle la manière dont nous communiquons ! Si mon père me demande de mettre la table, il va me donner (en entrée) des assiettes, je vais mettre la table et lui dire (en sortie) : « La table est mise ! ».
Reprenons Microsoft Word et l’action d’enregistrer un document. Lorsque vous cliquez sur « Enregistrer », Word prend (en entrée) le contenu non enregistré (texte, images…), l’enregistre, puis vous affiche un message de confirmation (en sortie).
Les actions effectuées par un programme sont des instructions.
On distingue trois grandes catégories d’instructions :
- Les opérations de base : addition, soustraction, multiplication, division… Exemple : « tire » + « – » + « bouchon » => « tire-bouchon ».
- L’exécution conditionnelle : si (condition), alors (fais ça), sinon (fais ça). Exemple : si je suis connectée, affiche « Salut Céline ! ».
- L’itération : répéter une instruction, un nombre déterminé de fois. Exemple : affiche chaque photo de mon album « Les rappeurs de Neuilly ».
En résumé
- Un algorithme est une suite d’instructions à suivre pour résoudre un problème.
- Chaque appareil informatique utilise des algorithmes pour exécuter ses fonctions sous la forme de logiciels ou d’applications.
- Les algorithmes prennent l’entrée et exécutent l’ensemble des instructions avec cette information pour générer une sortie.
- Un programme est essentiellement créé à l’aide d’un ensemble d’algorithmes.
Vous avez découvert dans ce chapitre la manière dont fonctionne un programme, et notamment l’intérêt des algorithmes dans un programme. Découvrez dans le prochain chapitre comment le structurer en résolvant un problème !
Découvrez l’intérêt des algorithmes
Une fois n’est pas coutume, commençons par nous demander quel est l’intérêt d’apprendre l’algorithmique, et surtout quels sont les différents sujets couverts par le domaine.
Le monde de l’informatique regorge de mots à la mode : IA, machine learning, cloud, informatique quantique, etc. Un mot en particulier est utilisé partout en informatique, c’est algorithme.
Concrètement, les algorithmes sont simplement une série d’instructions qui sont suivies, étape par étape, pour faire quelque chose d’utile ou résoudre un problème. Vous pourriez considérer une recette de gâteau comme un algorithme pour faire un gâteau, par exemple.
Alors pourquoi relions-nous toujours ce mot à l’informatique, et aux ordinateurs en particulier ? Tout simplement parce qu’un algorithme est avant tout un ensemble de méthodes utilisées par un ordinateur pour résoudre un problème. En fait, vous allez réfléchir aux différentes manières de résoudre un problème, puis faire en sorte que l’ordinateur le fasse pour vous. Pourquoi ? Ce n’est pas uniquement parce que nous sommes des fainéants ! Un ordinateur a des capacités étendues que nous, humains, ne pouvons égaler.
Avant tout, il ne se plaindra pas si vous lui demandez de réaliser des actions répétitives. Au contraire ! Déplacer vos 2 000 dernières photos de voyage une à une ? Facile ! Chercher dans ce PDF de 200 pages toutes les occurrences de l’expression « max tout puissant » ? Du gâteau ! Imaginez si vous deviez en faire de même ! Transférer 2 000 photos d’un album papier à un autre vous ennuierait à mourir…
Une seconde raison, et non des moindres : l’ordinateur va bien plus vite que nous. Il est plus efficace ! Essayez de calculer mentalement 10 x 20 x 30 x 40, et comparez votre temps de calcul à celui d’un ordinateur. Imbattable !
Décomposons la vie de tous les jours sous forme d’algorithme
Nous utilisons tous les jours des algorithmes quand nous avons plusieurs possibilités à étudier et qu’il nous faut faire un choix. Prenons un exemple. Vous allez rendre visite à votre grand-mère, mais, cornebleu, il y a des travaux sur la route et vous devez changer votre trajet habituel. Aujourd’hui, vous lanceriez très certainement votre GPS pour que l’ordinateur, notre ami, vous indique quelle est la route la plus rapide pour bien vite manger la tarte aux pommes qui doit déjà être sortie du four (il y a certaines priorités dans la vie !).
Qu’auriez-vous fait sans ordinateur ? Vous auriez déplié une carte papier et déterminé l’itinéraire idéal en prenant en compte certains paramètres : vitesse maximale autorisée sur chaque portion de route, péages, position actuelle. Vous auriez ensuite choisi le trajet le plus rapide en fonction de tous ces paramètres.
Bravo, vous pourriez remplacer l’ordinateur ! Mais vous auriez certainement réfléchi dix bonnes minutes… laissant ainsi à la tarte le temps de refroidir, seule et abandonnée dans la cuisine de votre grand-mère.
Heureusement, des informaticiens ont confectionné un algorithme et l’ont implémenté dans le petit boîtier sur votre pare-brise !
Les algorithmes du quotidien
Pourquoi apprendre l’algorithmique ? Car ses concepts vous ouvrent des portes vers bien des domaines, allant de la recherche en ligne à la conception de jeux vidéo.
Le tri algorithmique des sites web
Vous avez certainement remarqué que Facebook adapte votre fil d’actualité en fonction de votre activité. Votre page d’accueil n’affiche pas les dernières publications de vos amis, mais bien ce que Facebook considère comme étant le contenu le plus pertinent pour vous, compte tenu de votre activité.
Vous souhaitez en savoir plus ? Découvrez le cours Lancez une campagne Facebook Ads dans lequel vous sera expliqué en détail le fonctionnement de cet algorithme.
De même, lorsque vous effectuez une recherche sur Google, vous vous attendez à ce que la page affiche les résultats les plus pertinents, et non les derniers sites parus sur le domaine. Google a donc besoin d’un modèle pour déterminer comment calculer la pertinence de ces résultats en prenant en compte plusieurs paramètres tels que votre historique de recherche, le nombre de visites sur un site, le nombre de liens pointant vers le site, etc.
Ces deux exemples utilisent des méthodes de machine learning (ou apprentissage automatique) extrêmement intéressantes.
Pour en savoir plus, je vous conseille cette excellente vidéo de David Louapre (Science étonnante), Découvrir le machine learning et le deep learning, et surtout l’excellent cours de Yannis Chaouche, Initiez-vous au Machine Learning.
Les algorithmes appliqués à la géolocalisation
Votre GPS intègre un algorithme qui lui permet de déterminer le plus court chemin entre votre position actuelle et celle que vous lui avez indiquée. De même, les nombreux sites de réservation en ligne intègrent un algorithme qui gère les places libres dans un train, mais également les correspondances et les problèmes éventuels (annulation, par exemple).
Les algorithmes sont également utilisés dans des logiciels de reconnaissance d’image ou par votre banque lorsque vous effectuez des paiements sur Internet (détection de fraude). C’est très puissant !
Nous pourrions trouver bien plus d’exemples d’algorithmes intégrés à notre vie quotidienne. Leur point commun : répondre à une problématique que nous nous posons par l’utilisation d’un programme.
Qu’est-ce qu’un programme ?
Un programme est un ensemble d’instructions exécutables par un ordinateur et qui permet à ce dernier de répondre à un problème que nous nous posons. Un programme est essentiellement créé à l’aide d’un ensemble d’algorithmes. Par exemple, imaginons que je souhaite écrire une nouvelle version du dernier box-office de l’année. Je peux bien sûr utiliser une feuille et un crayon, mais comment la partager avec des amis ? Que se passe-t-il si je renverse mon café dessus ? Si un ami perd le manuscrit ? Etc. Après avoir pleuré toutes les larmes de mon corps, et m’être juré de ne plus boire de café ni de fréquenter d’humains pendant le restant de mes jours, je vais certainement allumer mon ordinateur et utiliser Microsoft Word.
D’ailleurs, comment fonctionne un programme ? De manière assez simple : il prend un ensemble de données en entrée, exécute des instructions puis retourne des données en sortie.
Tiens, cela me rappelle la manière dont nous communiquons ! Si mon père me demande de mettre la table, il va me donner (en entrée) des assiettes, je vais mettre la table et lui dire (en sortie) : « La table est mise ! ».
Reprenons Microsoft Word et l’action d’enregistrer un document. Lorsque vous cliquez sur « Enregistrer », Word prend (en entrée) le contenu non enregistré (texte, images…), l’enregistre, puis vous affiche un message de confirmation (en sortie).
Les actions effectuées par un programme sont des instructions.
On distingue trois grandes catégories d’instructions :
- Les opérations de base : addition, soustraction, multiplication, division… Exemple : « tire » + « – » + « bouchon » => « tire-bouchon ».
- L’exécution conditionnelle : si (condition), alors (fais ça), sinon (fais ça). Exemple : si je suis connectée, affiche « Salut Céline ! ».
- L’itération : répéter une instruction, un nombre déterminé de fois. Exemple : affiche chaque photo de mon album « Les rappeurs de Neuilly ».
En résumé
- Un algorithme est une suite d’instructions à suivre pour résoudre un problème.
- Chaque appareil informatique utilise des algorithmes pour exécuter ses fonctions sous la forme de logiciels ou d’applications.
- Les algorithmes prennent l’entrée et exécutent l’ensemble des instructions avec cette information pour générer une sortie.
- Un programme est essentiellement créé à l’aide d’un ensemble d’algorithmes.
Vous avez découvert dans ce chapitre la manière dont fonctionne un programme, et notamment l’intérêt des algorithmes dans un programme. Découvrez dans le prochain chapitre comment le structurer en résolvant un problème !
Posez les fondations
Comment se construit un programme ? Comme tout bâtiment : brique après brique et pas à pas.
La première étape consiste à découper notre grand problème en sous-problèmes. Imaginons que vous vouliez réaliser votre propre château en Lego. Vous avez toutes les pièces sous les yeux, mais vous ne savez pas encore dans quel ordre les assembler. Plutôt que de chercher à tout construire en même temps, ce qui serait impossible, vous débutez par un angle. Peut-être commencerez-vous par les fondations, ou par les fenêtres, ou pourquoi pas par le toit ? De toute manière, vous allez décomposer le château en plusieurs sous-ensembles.
C’est exactement ce que nous ferons dans ce chapitre en réfléchissant aux différentes règles de notre labyrinthe.
Règles du programme
Voici les règles de notre programme :
- Le joueur commence la partie sur la case “Départ”, et doit rejoindre la case “Arrivée”.
- Le joueur peut se déplacer uniquement dans quatre sens : haut, bas, droite et gauche.
- Le joueur devra ramasser des objets tout au long de son périple dans le labyrinthe pour s’assurer de sortir du labyrinthe.
- Le joueur a deux possibilités de jeu, soit un nombre de pas illimité, soit un nombre limité de pas.
Oublions l’ordinateur un moment, et réfléchissons à la manière dont nous pourrions construire ce jeu. Un algorithme n’étant qu’une solution à un problème, nous pouvons nous passer de nos amis les robots quelques instants.
Découper un problème en sous-problèmes
Quelles sont les opérations à réaliser par le joueur ?
Listons-les en bloc :
- Gérer les déplacements (haut, bas, gauche et droite).
- Enregistrer le nombre de déplacements.
- Compter le nombre de déplacements (un nombre de déplacements limité ou illimité).
- Stocker les objets ramassés.
Parfait. Nous avons une bonne feuille de route !
Décrire un algorithme avec le pseudo-code
Maintenant que nous avons pu découper notre problématique, comment allons-nous décrire les algorithmes qui vont résoudre ces sous-problèmes ?
C’est là qu’entre en jeu le pseudo-code, ou LDA (langage de description d’algorithmes). Le pseudo-code est une manière informelle de décrire la programmation, qui ne nécessite aucune syntaxe de langage de programmation stricte, ni aucune considération technologique sous-jacente. Il est utilisé pour créer l’ébauche ou le brouillon d’un programme.
Tout au long du cours, vous allez voir comment décrire chaque nouveau concept de la programmation à l’aide du pseudo-code. Mais commençons pour l’instant par voir un exemple simple de pseudo-code pour décrire les déplacements du joueur. Cela vous permettra de vous familiariser avec la syntaxe.
Il n’existe aucune norme standard pour la syntaxe du pseudo-code, car ce n’est pas un programme exécutable. Cependant, certaines normes limitées existent, mais qui peuvent varier en fonction des personnes.

Voici le pseudo-code qui décrit les déplacements du joueur du point de départ jusqu’à l’arrivée :
Algorithme déplacement
Début
Déplacement à droite
Déplacement en haut
Déplacement à droite
Déplacement en haut
Fin
Comment faut-il lire ce pseudo-code ?
- Le nom de l’algorithme est suivi du mot “Algorithme”.
- Deux mots-clés permettent de délimiter le début et la fin de l’algorithme :
DébutetFin. - Les instructions de l’algorithme se trouvent entre les mots-clés
DébutetFin.
À vous de jouer

Contexte
Au fil des chapitres, vous allez développer des algorithmes pour faire agir votre personnage dans le labyrinthe. Pour cette étape, l’objectif est de mener votre personnage du point de départ à l’arrivée.
Voici le labyrinthe en question :

Consignes
Vous pouvez utiliser les instructions suivantes dans votre algorithme pour décrire les déplacements :
- Déplacement à droite.
- Déplacement à gauche.
- Déplacement en haut.
- Déplacement en bas.
Écrivez les deux algorithmes possibles pour décrire le trajet du point de départ à l’arrivée !
Vérifiez votre travail
Voici les deux solutions possibles pour atteindre votre objectif :
Solution 1 :
Algorithme solution 1
Début
Déplacement à droite
Déplacement à droite
Déplacement à droite
Déplacement en haut
Déplacement en haut
Déplacement en haut
Fin
Solution 2 :
Algorithme solution 2
Début
Déplacement en haut
Déplacement en haut
Déplacement à droite
Déplacement en haut
Déplacement à droite
Déplacement à droite
Fin
En résumé
- Pensez à découper votre problème complexe en sous-problèmes plus simples à résoudre.
- Utilisez le pseudo-code pour décrire votre algorithme.
- Le pseudo-code est simplement une implémentation d’un algorithme sous la forme d’annotations et de texte informatif écrit en langage clair.
- Les instructions d’un pseudo-code sont délimitées par les mots-clés
DébutetFin.
Comment communiquer avec un ordinateur ?
Grâce à un langage de programmation, pardi ! Rendez-vous au prochain chapitre pour le découvrir.
Communiquez avec un ordinateur
Pour communiquer avec un ordinateur, vous avez d’abord besoin d’un langage. Entre humains, il existe beaucoup de langues différentes qui ont chacune leur usage. Nous avons d’ailleurs plusieurs familles de langues organisées souvent autour d’un alphabet : les langues indo-européennes (dont le français, l’espagnol ou l’anglais), les langues sino-tibétaines (dont le mandarin), les langues sémitiques (dont l’arabe), etc.
Ces langues partagent très souvent bien plus qu’un alphabet. Vous voyez où je veux en venir : par exemple, en français nous utilisons des verbes quand nous voulons exprimer une action. On utilise aussi des noms pour désigner les objets ou les personnes : une chaise, un tableau, une fille.
Les langages de programmation utilisent une logique très semblable. Dans ce cours, nous nous intéresserons à la programmation structurée qui est un des paradigmes de programmation les plus connus.
Un paradigme est une manière de concevoir une situation à la fois dans ses problématiques et dans les différentes solutions à apporter.
En programmation structurée, nous découpons un problème en micro tâches indépendantes les unes des autres, et modulaires. C’est exactement ce que nous sommes en train de faire !
Les noms : les variables
Une variable est une manière de faire référence à un objet. Dans le langage courant, c’est exactement ce que nous appelons « nom ». Qu’est-ce qu’un mot, sinon une étiquette que nous avons collée sur un objet pour pouvoir y faire référence plus tard ? Une variable a donc une valeur, et un mot qui permet d’accéder à cette valeur. Vous pouvez donc soit lire la valeur soit la modifier.
Nous pouvons par exemple créer deux variables dans notre algorithme pour compter le nombre de déplacements et le score du joueur, qu’on aura initialisés à 0 au début du programme.
Vous pouvez déclarer l’ensemble des variables dans le pseudo-code dans une section dédiée aux variables ; cela permet de donner une indication des différentes variables de l’algorithme. Vous placerez cette section juste avant le mot-clé Début , comme ceci :
Algorithme DéclarerVariable
Variable
déplacement ← 0
score ← 0
Début
Fin
Mettons-nous d’accord sur la manière de mettre à jour les variables, à travers ce tableau qui résume les différentes possibilités :
| Action | Variable | Valeur ajoutée |
| un déplacement | déplacement | +1 |
| un déplacement à droite | score | +10 |
| un déplacement à gauche | score | +20 |
| un déplacement en haut | score | +10 |
| un déplacement en bas | score | +20 |
Prenons le labyrinthe ci-dessous, et essayons de construire l’algorithme qui permet de rejoindre la case d’arrivée. Il faudra prendre en compte la mise à jour de chaque variable.

Voici le pseudo-code :
Algorithme variable
Variable
déplacement ← 0
score ← 0
Début
Déplacement à droite
déplacement ← déplacement + 1
score ← score + 10
Déplacement en haut
déplacement ← déplacement + 1
score ← score + 10
Déplacement en haut
déplacement ← déplacement + 1
score ← score + 10
Déplacement à gauche
déplacement ← déplacement + 1
score ← score + 20
Fin
Ainsi, à la fin du jeu, la variable déplacement contient la valeur 4, et la variable score contient la valeur 50.
Les verbes : les fonctions
À présent, voyons comment simplifier la mise à jour des deux variables en regroupant les instructions dans un seul même bloc. Vous avez sûrement pu le remarquer, nous avons dû écrire plusieurs fois les instructions qui permettent de changer les valeurs des deux variables.
Nous allons utiliser ce qu’on appelle, en programmation, une fonction. Il s’agit d’un bloc qui regroupe plusieurs actions. Vous pouvez réutiliser ce bloc autant de fois que vous le voulez en invoquant son nom. Une fonction peut aussi être vue comme une moulinette qui va prendre des informations en entrée, les traiter et en renvoyer d’autres en sortie. C’est en quelque sorte un mini-algorithme.
Lorsqu’une fonction est « appelée », le programme « quitte » la section de code en cours et commence à exécuter la première ligne à l’intérieur de la fonction.
Nous allons maintenant créer notre fonction à partir des critères suivants :
| Nom | maj_déplacement_score |
| Paramètres d’entrée | déplacementscorepoint_de_déplacement (point en fonction du sens de déplacement) |
| Instructions | Ajouter +1 à la variable déplacementIncrémenter la variable score à l’aide du paramètre point_de_déplacement |
| Paramètres de sortie | Pas de paramètre de sortie |
Nous pouvons décrire cette fonction à l’aide du pseudo-code :
Fonction maj_déplacement_score(déplacement, score, point_de_déplacement)
Début
déplacement ← déplacement + 1
score ← score + point_de_déplacement
Fin
Vous remarquerez qu’il n’y a pas de différence avec la description d’un algorithme en pseudo-code, sauf que nous avons ajouté entre parenthèses les paramètres d’entrée. Vous pouvez ajouter avant la fin de la fonction, avec le mot-clé Retourner , les valeurs de sortie, s’il y en a.
En langage informatique, la création d’une fonction est ce que nous appelons une déclaration. Son utilisation est son exécution.
Nous utiliserons la fonction maj_déplacement_score pour modifier notre algorithme précédent ainsi :
Algorithme variable
Variable
déplacement ← 0
score ← 0
Début
Déplacement à droite
maj_déplacement_score(déplacement, score, 10)
Déplacement en haut
maj_déplacement_score(déplacement, score, 10)
Déplacement en haut
maj_déplacement_score(déplacement, score, 10)
Déplacement à gauche
maj_déplacement_score(déplacement, score, 20)
Fin
À vous de jouer

Contexte
Reprenons notre périple dans le labyrinthe.
Considérons le pseudo-code suivant qui dirige les déplacements du joueur dans le labyrinthe :
Algorithme déplacement
Variable
déplacement ← 0
score ← 0
Début
Déplacement en haut
Déplacement en haut
Déplacement à droite
Déplacement à gauche
Déplacement en bas
Déplacement en bas
Fin
Vous allez mettre en place dans cet exercice une fonction permettant de calculer votre score selon le nombre de déplacements effectués.

Consignes
Reprenez le pseudo-code ci-dessus et adaptez-le en fonction des consignes suivantes :
- Un déplacement incrémente la variable
déplacementde 1. - Incrémentation du
scoreen fonction du sens de déplacement :- à gauche :
50 points / le nombre de déplacements - à droite :
70 points / le nombre de déplacements - en haut :
25 points / le nombre de déplacements - en bas :
90 points / le nombre de déplacements
- à gauche :
- Si le joueur passe à nouveau sur une même case, il faut décrémenter le score de 25 points.
- Si le joueur revient à la case Départ, le
scoreest réinitialisé à 0.
Votre objectif :
- Créez l’algorithme qui prend en compte l’ensemble des consignes ci-dessus. N’hésitez pas à écrire à côté de chaque instruction la valeur courante des variables
déplacementetscore. - Créez une fonction qui permet de mettre à jour les variables
déplacementetscore. - Créez une fonction qui permet de réinitialiser la variable
scoreà 0. - Adaptez votre algorithme avec les deux nouvelles fonctions.
Vérifiez votre travail
Voici les quatre étapes à suivre pour obtenir le résultat final de cet exercice :
Première étape : création de l’algorithme de déplacement
Algorithme déplacement
Variable
déplacement ← 0
score ← 0
Début
Déplacement en haut
déplacement ← déplacement + 1
score ← score + 25
Déplacement en haut
déplacement ← déplacement + 1
score ← score + 25
Déplacement à droite
déplacement ← déplacement + 1
score ← score + 70
Déplacement à gauche
déplacement ← déplacement + 1
score ← score + 50 - 25 (Le joueur revient sur une case)
Déplacement en bas
déplacement ← déplacement + 1
score ← score + 90 - 25 (Le joueur revient sur une case)
Déplacement en bas
déplacement ← déplacement + 1
score ← score + 90 - 25 (Le joueur revient sur une case)
score ← 0 (Le joueur est revenu à la case départ donc score = 0)
Fin
Seconde étape : création de la fonction de mise à jour des variables déplacement et score
Fonction maj_déplacement_score(déplacement, score, point_de_déplacement)
Début
déplacement ← déplacement + 1
score ← score + (point_de_déplacement / déplacement)
Fin
Troisième étape : création de la fonction de réinitialisation du score
Fonction réintialiser_score(score)
Début -
score ← 0
Fin
Quatrième étape : adaptation de l’algorithme avec les deux fonctions précédentes
Algorithme déplacement
Variable
déplacement ← 0
score ← 0
Début
Déplacement à droite
maj_déplacement_score(déplacement, score, 25)
Déplacement en haut
maj_déplacement_score(déplacement, score, 25)
Déplacement en haut
maj_déplacement_score(déplacement, score, 70)
Déplacement en bas
maj_déplacement_score(déplacement, score, 25 - 25)
Déplacement en bas
maj_déplacement_score(déplacement, score, 90 - 25)
Déplacement à gauche
maj_déplacement_score(déplacement, score, 90 - 25)
réintialiser_score(score)
Fin
En résumé
- La plupart des langages de programmation ont une structure de base similaire les uns aux autres.
- Les variables sont utilisées pour stocker des informations à référencer et à manipuler dans un programme informatique.
- Une fonction est simplement un « morceau » de code que vous pouvez réutiliser, plutôt que de le réécrire plusieurs fois.
- Les fonctions « prennent » généralement des données en entrée, les traitent et « renvoient » un résultat.
Vous avez découvert le monde des variables et comment simplifier votre algorithme en le découpant en fonctions. Il est maintenant temps de tester vos connaissances à l’aide d’un petit quiz dans le chapitre suivant. Bonne chance !
Décrire le fonctionnement d’un algorithme
Compétences évaluées
- Décrire le fonctionnement d’un algorithme
Description
Dans ce quiz, vous allez construire, au fur et à mesure des questions, un algorithme regroupant ce que vous avez appris dans cette première partie. Il s’agit d’un algorithme représentant toutes les étapes pour cuisiner un gâteau au chocolat.
- Question 1Quelle situation de la vie réelle peut être assimilée à un algorithme ?Attention, plusieurs réponses sont possibles.
- Aller jusqu’au magasin
- Additionner 2 + 2
- Cuisiner un gâteau
- Mettre le four à préchauffer
- Question 2Avant de nous lancer dans la cuisine, il est important de bien différencier les instructions de l’algorithme. Parmi ces réponses, lesquelles sont des instructions ?Attention, plusieurs réponses sont possibles.
- préparer le gâteau
- préparer la pâte
- enfourner la pâte
- mélanger la pâte
- Question 3À partir de maintenant, nous allons préparer un gâteau au chocolat en nous servant d’un algorithme que vous allez concevoir pas à pas.Commençons par prendre un sachet de gâteau au chocolat, prêt à cuire. Nous devons simplement verser le contenu du sachet dans un moule, préchauffer le four et ensuite l’enfourner. Combien d’instructions sont-elles nécessaires pour cuisiner ce gâteau au chocolat ?
- 1
- 3
- 5
- 7
- Question 4Reprenons les étapes de la question précédente.Comment pouvez-vous représenter le problème sous la forme d’un algorithme décrit en pseudo-code ?
1) Verser le contenu dans un moule 2) Préchauffer le four 3) Enfourner le mouleAlgorithme RecetteGâteau - Verser le contenu dans un moule - Préchauffer le four - Enfourner le mouleAlgorithme RecetteGâteau Début Verser le contenu dans un moule Préchauffer le four Enfourner le moule Fin
- Question 5Cette fois, vous allez devoir mettre les mains à la pâte ! Nous allons corser les choses, et vous n’allez pas vous contenter d’un sachet de gâteau prêt à cuire.Voici la vraie recette du gâteau au chocolat :
- Dans une casserole, faites fondre le chocolat et le beurre coupés en morceaux à feu doux, et mélangez bien.
- Dans un saladier, ajoutez le sucre, les œufs, la farine, et mélangez le tout. Ensuite, beurrez votre moule à l’aide d’une feuille de papier essuie-tout, et farinez le moule avant d’y verser la pâte à gâteau.
- Pour terminer, préchauffez votre four à 180°C et faites cuire au four environ 30 minutes.
-
- Faites fondre le chocolat et le beurre à feu doux.
- Ajoutez dans un saladier, sucre, oeufs et farine.
- Beurrez et farinez le moule.
- Versez la pâte à gâteau.
- Faites cuire au four 30 minutes.
-
- Faites fondre le chocolat et le beurre à feu doux.
- Ajoutez dans un saladier, sucre, oeufs et farine.
- Mélangez.
- Beurrez et farinez le moule.
- Versez la pâte à gâteau.
- Préchauffez le four à 180°C.
- Faites cuire au four 30 minutes.
-
- Faites fondre le chocolat et le beurre à feu doux.
- Mélangez.
- Ajoutez dans un saladier, sucre, oeufs et farine.
- Mélangez.
- Beurrez et farinez le moule.
- Versez la pâte à gâteau.
- Préchauffez le four à 180°C.
- Faites cuire au four 30 minutes.
- Question 6Maintenant, nous souhaitons découper notre algorithme en sous-problèmes, c’est-à-dire que nous allons découper notre algorithme en plusieurs parties. Chacune de ces parties appelées sous-problèmes contiendra une série d’instructions. Pour cela, nous allons créer un algorithme qui sera responsable de la préparation de la pâte à gâteau, et un autre de la cuisson de cette pâte.Quels sous-algorithmes correspondent au découpage de notre algorithme global ?
Algorithme PâteAGâteau Début Faites fondre le chocolat et le beurre Mélangez Ajoutez dans un saladier sucre, oeufs et farine Mélangez Versez la pâte à gâteau dans le moule Fin Algorithme Cuisson Début Préchauffez le four à 180°C Enfournez le moule FinAlgorithme PâteAGâteau Début Faites fondre le chocolat et le beurre Mélangez Ajoutez dans un saladier sucre, oeufs et farine Fin Algorithme Cuisson Début Mélangez Versez la pâte à gâteau dans le moule Préchauffez le four à 180°C Enfournez le moule FinAlgorithme PâteAGâteau Début Faites fondre le chocolat et le beurre Mélangez Ajoutez dans un saladier sucre, oeufs et farine Mélangez Versez la pâte à gâteau dans le moule Préchauffez le four à 180°C Fin Algorithme Cuisson Début Enfournez le moule Fin
- Question 7Nous souhaitons enregistrer dans une variable la température de cuisson et le temps de cuisson.Quelle méthode dans le pseudo-code permet de déclarer les variables avant le début de l’algorithme ?
Algorithme Cuisson temperature ← 180 temps_cuisson ← 30 Début . … FinAlgorithme Cuisson Variable temperature ← 180 temps_cuisson ← 30 Début . … FinAlgorithme Cuisson Début . … Fin Variable temperature ← 180 temps_cuisson ← 30
- Question 8Pour terminer, nous souhaitons créer une fonction
cuissonqui prend en paramètre la température de préchauffage et le temps de cuisson, et qui appelle deux fonctions :préchauffage: cette fonction prend en paramètre la température de préchauffage.enfournage: cette fonction prend en paramètre le temps de cuisson.
cuisson?Algorithme cuisson(temperature_préchauffage, temps_cuisson) Début préchauffage(temperature_préchauffage) enfournage(temps_cuisson) FinAlgorithme cuisson() Début préchauffage(temperature_préchauffage) enfournage(temps_cuisson) FinAlgorithme cuisson(temperature_préchauffage, temps_cuisson) Début préchauffage() enfournage() Fin
Découvrez les types de données les plus fréquents
Nous, en tant qu’humains, nous sommes capables de faire la différence entre 12 qui est un nombre, et bonjour , un mot écrit avec des lettres. Cependant, un ordinateur ne le comprend pas tout seul. Du moins, pas sans une petite aide de notre part : nous devons lui préciser le type de la valeur pour qu’il puisse la lire et la comprendre. En effet, le type d’une variable permet de spécifier plusieurs paramètres nécessaires à l’ordinateur, par exemple :
- la taille ;
- la disposition de la mémoire de la variable ;
- la plage de valeurs pouvant être stockées dans cette mémoire ;
- l’ensemble des opérations pouvant être appliquées à la variable.
Un type de données est une classification de données qui indique à l’ordinateur comment le programmeur a l’intention d’utiliser les données.
Il existe plusieurs types de variables, et jusqu’à maintenant nous avons manipulé seulement un type de données, les nombres. Mais il est tout à fait possible d’utiliser d’autres types de données, tels que les mots et les booléens, deux autres types fréquemment utilisés en programmation.
Un booléen est un type de données avec deux valeurs possibles : vrai ou faux. Une condition est souvent évaluée en tant que booléen – la condition EST vraie ou fausse.
Vous n’allez pas diviser un mot par cinq, par exemple ! Ou mettre un nombre en majuscules ! Mais l’ordinateur ne voit pas la différence entre les deux. C’est pourquoi nous attribuons des types aux différents concepts que nous manipulons dans un programme.
Nous pouvons les visualiser comme étant des pièces de Lego. Certaines sont des plaques plates et larges pour le sol, d’autres des ronds pour fabriquer un mât ou des charnières de porte. Certaines pièces ont une utilité spécifique, mais ce sont toutes des Lego !
Les nombres
Tout comme en mathématiques, il existe plusieurs sortes de nombres, qui sont regroupés sous le doux nom de « nombres décimaux ». Les nombres décimaux peuvent être entiers (pas de virgules, integer, en anglais) ou à virgules (float, en anglais).
Nombres entiers : 1 ; 5 ; 10. Nombres à virgule : 1,3 ; 1,7777 ; 2,3.
En informatique, il est assez compliqué de représenter des nombres qui contiennent une infinité de chiffres après la virgule, comme pi ou 1/3. Chaque langage propose des solutions différentes.
Les chaînes de caractères
Une chaîne de caractères est composée d’un ensemble de caractères pouvant également contenir des espaces et des chiffres. Par exemple : « a », « Algorithme » et « J’ai 2 frères ».
Dans un programme ou dans le pseudo-code, les chaînes de caractères sont généralement écrites entre guillemets, comme ceci : “Une chaîne de caractères”. Cette méthode permet de déterminer le début et la fin de la chaîne de caractères.
Les booléens
Enfin, notre petit dernier est un type de données qui indique « Vrai » ou « Faux ». Vous pouvez vous le représenter comme un interrupteur, ou une carte qui aurait deux faces : « Vrai » et « Faux », ou en anglais, “True” et “False”.
Mais vous allez me dire : à quoi cela sert-il donc ?
À utiliser des conditions ! Lorsque vous vérifiez une condition, c’est une information de type booléen qui est donnée en réponse.
Vous pouvez maintenant ajouter cette information dans la section des variables lors de la déclaration d’une variable. Vous pouvez placer après la variable le type de cette donnée.
| ENTIER | Un nombre entier |
| FLOAT | Un nombre à virgule |
| CHAÎNE DE CARACTÈRES | Une chaîne de caractères |
| BOOL | Un booléen |
Voilà ce que ça peut donner sur le pseudo-code :
Algorithme Type
Variable
nombreEntier ← 0 : ENTIER
nombreFlottant ← 0.0 : FLOAT
ChaineDeCaractères : CHAINE DE CARACTÈRES
booléen ← Faux : BOOL
Vous avez pu remarquer qu’il n’y a pas grand chose qui change dans la déclaration des variables, il suffit d’ajouter le type de la variable précédé de deux points : .
À vous de jouer

Contexte
Considérons l’algorithme suivant qui appelle la fonction déplacementDépartArrivée qui déplace le joueur de la case Départ à la case d’arrivée automatiquement :
Algorithme Labyrinthe
Début
déplacementDépartArrivée()
Fin
Consigne
Vous devez créer deux variables :
- La première enregistrera le nom du joueur.
- La seconde permettra de savoir si le joueur a terminé le labyrinthe.
De plus, la fonction déplacementDépartArrivée devra prendre le nom du joueur en paramètre pour correctement fonctionner.
Votre objectif :
- Déclarer la variable
nomDuJoueur, l’initialiser et ajouter son type de donnée. - Au début de l’algorithme, assigner votre nom à la variable
nomDuJoueur. - Ajouter la variable
nomDuJoueuren paramètre de la fonctiondéplacementDépartArrivée. - Déclarer la variable
est_terminé, l’initialiser àfauxet ajouter son type de donnée. - Changer la valeur de la variable
est_terminési nécessaire dans l’algorithme.
Vérifiez votre travail
Voici le résultat à obtenir à l’issue de l’exercice :
Algorithme Labyrinthe
Variable
nomDuJoueur ← "" : CHAINE DE CARACTÈRES
est_terminé ← Faux : BOOL
Début
nomDuJoueur ← "Ranga"
déplacementDépartArrivée(nomDuJoueur)
est_terminé ← Vrai
Fin
En résumé
- Une variable peut être considérée comme un emplacement de mémoire pouvant contenir des valeurs d’un type spécifique.
- Chaque variable a un type de donnée spécifique, qui indique le type de donnée qu’elle peut contenir.
- Il existe des types pour stocker des nombres, des chaînes de caractères et des booléens.
- Le type de la variable peut être spécifié dans le pseudo-code dans la section
variableafin de donner plus d’informations sur la variable.
Maintenant que vous connaissez les différents types de données, vous ne pouvez plus vous tromper sur le choix du type de votre variable. Effectivement, ce choix sera crucial pour la suite du programme, et surtout pour ce que vous souhaitez faire avec cette variable. Dans le chapitre suivant, nous allons voir comment lancer ou non certaines instructions grâce aux structures conditionnelles.
Découvrez les structures conditionnelles
Il arrive des situations dans la vie réelle où vous devez prendre des décisions, et sur la base de ces décisions, vous agissez en conséquence. Des situations similaires se produisent également dans la programmation où vous devez prendre des décisions en fonction d’une condition. C’est ainsi que vous pourrez lancer ou non certains blocs de code.
Revenons à notre programme et imaginons un scénario que nous n’avons pas vu jusqu’à maintenant. Nous souhaitons avoir une fonction qui nous permette d’afficher un message de victoire ou de défaite à la fin des déplacements. Plus simplement, si à la fin des déplacements, nous sommes sur la case d’arrivée, le programme affiche Vous avez gagné ! , sinon, le programme affiche Vous avez perdu ! .
Si
Le mot-clé Si (en anglais “if”) est la structure de test la plus simple. Il est utilisé pour décider si une instruction particulière ou un bloc d’instructions sera exécuté ou non. En clair, si une condition définie est vraie, alors un bloc d’instructions sera exécuté ; sinon, non.
Nous pouvons, par exemple, créer une structure Si qui vérifie si le joueur se trouve dans la case d’arrivée et si c’est le cas, on affiche Vous avez gagné ! .
Nous pouvons écrire le pseudo-code suivant :
Algorithme Si_structure
Début
Si le joueur est sur la case arrivée :
afficher `Vous avez gagné !`
Fin Si
Fin
Ainsi, dans cet algorithme, si le joueur est sur la case Arrivée, on affiche le messageVous avez gagné ! , sinon aucune instruction n’est lancée, donc nous n’avons pas de message.
En réalité, dans un algorithme, pour tester une condition nous allons utiliser des opérateurs de comparaison afin de comparer des paramètres du programme.
Pour effectuer ces tests, il existe des symboles utilisés dans la plupart des langages de programmation :
| Symbole | Signification |
| == | Est égal à |
| > | Est supérieur à |
| < | Est inférieur à |
| >= | Est supérieur ou égal à |
| <= | Est inférieur ou égal à |
| != | Est différent de |
Imaginons maintenant que nous ayons une variable qui contient les coordonnées du joueur sur le labyrinthe ( joueur_coordonnées ), et une variable qui contient aussi les coordonnées de la case d’arrivée ( arrivée_coordonnées ).
Nous pouvons alors remplacer notre pseudo-code par le suivant :
Algorithme Si_structure
Début
Si joueur_coordonnées == arrivée_coordonnées :
afficher `Vous avez gagné !`
Fin Si
Fin
Si… Sinon…
Néanmoins, nous avons toujours un problème. Comment allons-nous faire pour afficher le message de défaite ?
Cette fois nous avons besoin d’une autre structure conditionnelle, nous allons devoir combiner le mot-clé Si avec le mot-clé Sinon . En effet, le mot-clé Si seul nous dit que si une condition est vraie, elle exécutera un bloc d’instructions, et si la condition est fausse, elle ne le fera pas. Ainsi, nous devons utiliser le mot-clé Sinon avec Si pour exécuter un bloc de code lorsque la condition est fausse.
Dans le cas de notre labyrinthe, nous pouvons ajouter une structure conditionnelle à la fin de notre algorithme, qui nous permet de savoir si le joueur a gagné ou pas : si le joueur est sur la case Arrivée, dans ce cas, on affiche Vous avez gagné ! ; sinon, on affiche Vous avez perdu ! .
Algorithme Si_structure
Début
Si joueur_coordonnées == arrivée_coordonnées :
afficher `Vous avez gagné !`
Sinon
afficher `Vous avez perdu !`
Fin Si
Fin
Cette structure est également appelée « if/else », car l’anglais est souvent à la base des noms dans un langage de programmation.
Combinez des conditions
Pour les conditions les plus complexes, sachez que vous pouvez faire plusieurs tests au sein d’un seul et même Si . Pour cela, il va falloir utiliser de nouveaux mots-clés, ET et OU :
- L’opérateur
ETrenvoieVrailorsque ses conditions gauche et droite sont égalementVrai. Lorsqu’une ou les deux conditions sont fausses, le résultat obtenu parETest égalementFaux. - L’opérateur
OUrenvoieVrailorsque sa condition gauche, droite ou les deux sontVrai. La seule fois oùOUrenvoie False, c’est lorsque les deux conditions sont également fausses.
Testez ET
Imaginons que nous souhaitions ajouter une condition en plus pour notre message de fin de jeu. Cette fois, une fois que le joueur a fini ses déplacements, il faut vérifier que le joueur est sur la case d’arrivée et qu’il n’a pas fait plus de 10 déplacements.
Nous avons alors :
Algorithme operateur_ET
Début
Si joueur_coordonnées == arrivée_coordonnées ET déplacements <= 10 :
afficher `Vous avez gagné !`
Sinon
afficher `Vous avez perdu !`
Fin Si
Fin
Notre condition combinée se dirait en français : « Si les coordonnées du joueur et les coordonnées de la case arrivée sont égales ET si le nombre de déplacements est inférieur ou égal à 10».
Testez OU
Prenons cette fois le problème autrement, une fois que le joueur a fini ses déplacements. Nous allons afficher Vous avez perdu ! , si le joueur n’est pas sur la case d’arrivée ou que le joueur a fait plus de 10 déplacements.
Algorithme operateur_OU
Début
Si joueur_coordonnées != arrivée_coordonnées OU déplacements > 10 :
afficher `Vous avez perdu !`
Sinon
afficher `Vous avez gagné !`
Fin Si
Fin
À vous de jouer

Contexte
Pour le moment, nous n’avons pas créé de fonction qui permette de gérer les déplacements du joueur en fonction de la demande de l’utilisateur. C’est exactement ce que nous allons mettre en place maintenant.
Considérons que la fonction entrer() permet de demander à l’utilisateur d’entrer le sens de déplacement, et retourne l’entrée de l’utilisateur.
Voici les 4 cas possibles :
- “Haut” : déplacement vers le haut ;
- “Bas” : déplacement vers le bas ;
- “Droite” : déplacement vers la droite ;
- “Gauche” : déplacement vers la gauche.
Afin de pouvoir stocker le sens de déplacement entré par l’utilisateur, vous allez devoir stocker la valeur de retour de la fonction entrer() dans une variable, comme ceci par exemple :sens ← entrer()
Vous avez aussi besoin de deux variables qui permettent de stocker les coordonnées du joueur, position_x et position_y . Ces deux variables seront passées en paramètre de la fonction.
Voilà comment mettre à jour les coordonnées du joueur en fonction des déplacements :
| déplacement vers le haut | ajoutez 1 à y |
| déplacement vers le bas | retirez 1 à y |
| déplacement vers la droite | ajoutez 1 à x |
| déplacement vers la gauche | retirez 1 à x |
Nous avons alors ce début de pseudo-code :
Algorithme déplacement(position_x , position_y)
Variable
sens ← “” : CHAÎNE DE CARACTÈRES
Début
Fin
Consigne
Vous devez maintenant créer une fonction qui permette de modifier les déplacements du joueur dans le labyrinthe. En effet, cette fonction va demander à l’utilisateur d’entrer le sens de déplacement qu’il souhaite, et la fonction va modifier les coordonnées x et y du joueur en fonction du sens de déplacement.
Attention, vous allez devoir prendre en compte les erreurs de frappe de l’utilisateur : seules les chaînes de caractères prévues ci-dessus sont valables (“Haut”, “Bas”, “Droite” et “Gauche”).
Votre objectif :
- Demander à l’utilisateur d’entrer le sens de déplacement.
- Vérifier à l’aide d’une première structure conditionnelle si l’entrée de l’utilisateur est correcte en fonction des 4 possibilités. Sinon afficher un message qui stipule que l’entrée n’est pas correcte.
- Si l’entrée de l’utilisateur est correcte : à l’aide de plusieurs structures conditionnelles, vous allez devoir mettre à jour les coordonnées du joueur en fonction de l’entrée de l’utilisateur.
Vérifiez votre travail
Voici le résultat à obtenir à l’issue de l’exercice :
Algorithme déplacement(position_x , position_y)
Variable
sens ← “” : CHAÎNE DE CARACTÈRES
Début
sens ← entrer()
Si sens == “Haut” OU sens == “Bas” OU sens == “Droite” OU sens == “Gauche” :
Si sens == “Haut” :
position_y = position_y + 1
Fin Si
Si sens == “Bas” :
position_y = position_y - 1
Fin Si
Si sens == “Droite” :
position_x = position_x + 1
Fin Si
Si sens == “Gauche” :
position_x = position_x - 1
Fin Si
Sinon
afficher “L’entrée n’est pas correcte”
Fin Si
Fin
En résumé
- Les structures conditionnelles permettent de contrôler l’exécution ou non de certaines instructions.
- L’instruction
Siest utilisée pour exécuter le code si une condition est vraie. - L’instruction
if-elseest une version étendue de l’instructionSi. Grâce au mot-cléelse, vous pouvez choisir quelles instructions lancer si la condition n’est pas vraie. - Les mots-clés
ETetOUpermettent de combiner les conditions dans les structures conditionnelles.
Dans le chapitre suivant, nous allons partir à la découverte d’une notion très intéressante de la programmation : les boucles ! D’ailleurs, vous allez pouvoir continuer à travailler les conditions même sur les boucles. Allez, on y va !
Ajoutez une boucle
Comment faire pour réaliser une même action plusieurs fois ?
Dans le cas de notre système, nous souhaitons que l’utilisateur déplace son joueur pour terminer le jeu, sans connaître les déplacements ni le nombre de déplacements à l’avance.
Laissez-moi vous présenter les boucles !
Une boucle est une structure qui répète la même action plusieurs fois de suite. Exactement comme lorsque vous écoutez un morceau de musique en boucle.
Nous pouvons faire la même chose dans un algorithme. C’est ce qu’on appelle l’itération, qui nous permet « d’écrire du code une fois » et de « l’exécuter plusieurs fois ». Dans la programmation, on parle de boucle !
Dans la plupart des langages de programmation, nous utilisons principalement deux types de boucles : la boucle Tant que (en anglais, while ) et la boucle Pour (en anglais, for ).
- La boucle
Tant queest utilisée pour exécuter le corps de la boucle jusqu’à ce qu’une condition spécifique soit fausse. Nous appliquons principalement cette idée lorsque nous ne savons pas combien de fois la boucle s’exécutera. - Nous utilisons la boucle
Pourlorsque nous savons combien de fois la boucle s’exécutera. En d’autres termes, la bouclePournous aide à exécuter un nombre d’étapes défini par des instructions.
Utilisez la boucle Tant que
La boucle Tant que se compose :
- d’une condition de boucle ;
- d’un bloc de code en tant que corps de boucle, et qui contient les instructions à exécuter itérativement.
Concrètement, la condition de la boucle est évaluée et si elle est vraie, le code dans le corps de la boucle sera exécuté. Ce processus se répète jusqu’à ce que la condition de la boucle devienne fausse.
Ainsi, nous pouvons naïvement dire que la boucle while peut être considérée comme une instruction Si répétitive.
Voici le pseudo-code qui permet de déplacer le joueur dans le labyrinthe tant qu’il n’a pas atteint la case d’arrivée ; nous utiliserons la fonction déplacement créée dans le chapitre précédent :
Algorithme boucle_tant_que
Variable
joueur_position_x ← 0 : ENTIER
joueur_position_y ← 0 : ENTIER
arrivée_position_x ← 5 : ENTIER
arrivée_position_y ← 5 : ENTIER
Début
Tant Que joueur_position_x != arrivée_position_x ET joueur_position_y != arrivée_position_y :
déplacement(joueur_position_x, joueur_position_y)
Fin Tant Que
Fin
Grâce à cette boucle, vous n’avez plus besoin d’écrire manuellement dans l’algorithme chaque déplacement du joueur.
Vous vous dites sûrement que c’est super génial et super simple. Et c’est vrai, c’est le cas, mais il y a un “MAIS”.
Que se passe-t-il si vous demandez à lire en boucle une chanson ?
Elle pourra être jouée, potentiellement, jusqu’à la nuit des temps, car l’ordinateur ne sait pas quand il doit s’arrêter. C’est ce que nous appelons une boucle infinie ! Ainsi, si la condition de la boucle est toujours vraie, votre programme sera bloqué dans la boucle et ne s’arrêtera jamais !
Lorsque vous créez une boucle Tant que , pensez donc à y intégrer une condition d’arrêt afin qu’elle ne tourne pas à l’infini !
Utilisez la boucle “Pour”
À l’intérieur de la boucle Pour , nous utilisons une variable de boucle pour contrôler l’exécution de la boucle, où la valeur initiale de la variable décide du point de départ.
- Donc, nous commençons par initialiser la variable de boucle à une certaine valeur.
- Nous vérifions ensuite si la condition de boucle est vraie ou non.
- Si la condition de la boucle est vraie, le code à l’intérieur du corps de la boucle s’exécutera.
- Enfin, nous mettons à jour la variable de boucle et passons à l’itération suivante. Cette étape sera répétée jusqu’à ce que la condition de boucle devienne fausse.
Plus concrètement, la boucle Pour nécessite 3 instructions pour itérer :
- Initialisation de la variable de boucle.
- Condition d’itération.
- Mise à jour de la variable de boucle.
Nous pouvons par exemple imaginer que l’utilisateur doit exactement déplacer le joueur 10 fois.
Nous aurons ainsi le pseudo-code suivant :
Algorithme boucle_pour
Variable
joueur_position_x ← 0 : ENTIER
joueur_position_y ← 0 : ENTIER
max_déplacement ← 10 : ENTIER
Début
Pour i ← 0 ; i < max_déplacement; i = i + 1
déplacement(joueur_position_x, joueur_position_y)
Fin Pour
Fin
Dans ce pseudo-code, nous avons initialisé la variable de boucle i à 0, ensuite la condition de boucle permet de spécifier qu’il faut itérer le bloc de code tant que la variable i est inférieure au maximum de déplacements, et pour terminer nous mettons à jour la variable i en ajoutant 1.
Vous pouvez simplifier la ligne concernant la commande Pour de cette manière :
Pour i allant de 0 jusqu’à max_déplacement
À vous de jouer

Contexte
Actuellement dans notre labyrinthe, nous sommes obligés de préciser à l’avance chaque déplacement du joueur dans l’algorithme. Nous aimerions pouvoir laisser à l’utilisateur le choix des déplacements du joueur. Il va donc falloir utiliser une boucle pour demander à l’utilisateur quels déplacements il souhaite faire.
Consigne
Vous devez créer un algorithme qui permet de déplacer le joueur à l’aide de la fonction déplacement créée précédemment, de la case de départ à l’arrivée. Attention, le joueur aura au maximum 15 déplacements. Si le nombre de déplacements dépasse 15, le joueur perd.
Votre objectif :
- Créer une boucle qui permet de déplacer le joueur en prenant en compte la position du joueur et le nombre de déplacements.
- Créer ensuite une structure conditionnelle pour la boucle, pour afficher si le joueur a gagné ou perdu.
Vérifiez votre travail
Voici le résultat à obtenir à l’issue de l’exercice :
Algorithme Labyrinthe
Variable
joueur_position_x ← 0 : ENTIER
joueur_position_y ← 0 : ENTIER
arrivée_position_x ← 5 : ENTIER
arrivée_position_y ← 5 : ENTIER
déplacement ← 0 : ENTIER
max_déplacement ← 15 : ENTIER
Début
Tant Que joueur_position_x != arrivée_position_x ET joueur_position_y != arrivée_position_y ET déplacement < 15 :
déplacement(joueur_position_x, joueur_position_y)
déplacement = déplacement + 1
Fin Tant Que
Si joueur_position_x == arrivée_position_x ET joueur_position_y == arrivée_position_y :
afficher “Vous avez gagné !”
Sinon
afficher “Vous avez perdu !”
Fin Si
Fin
En résumé
- Pour résoudre un problème, nous répétons parfois une instruction de code particulière plusieurs fois jusqu’à ce qu’une condition spécifique soit satisfaite ; c’est ce qu’on appelle une boucle.
- Il existe deux principaux types de boucles dans la programmation, la boucle
Tant queet la bouclePour. - La boucle
Tant queest utilisée pour répéter une section de code un nombre inconnu de fois, jusqu’à ce qu’une condition spécifique soit remplie. - La boucle
Pourest utilisée pour répéter une section de code un nombre de fois connu.
Nous avions vu dans le premier chapitre de cette partie comment classer les données avec des types de données simples. Nous allons maintenant nous intéresser à des données complexes. On y va !
Découvrez les différents types de containers existants
Agencez les informations entre elles
Les différents types définis et utilisés dans un programme s’appellent des structures de données. Elles peuvent être comparées à des constructions en Lego qui ont un but assez particulier : roue, fenêtre, carrosse ou encore lac.
Il en est de même pour les structures de données en programmation. Nous serons vite limités si nous entrons les données une à une dans un algorithme. Nous aimerions parfois entrer plusieurs données déjà organisées d’une certaine manière, pour améliorer l’efficacité d’un algorithme. Ou bien nous aimerions générer une certaine structure pour qu’elle puisse être utilisée par ailleurs.
Une structure permet de stocker plusieurs données de même type ou de types différents dans un seul conteneur (la structure). Une structure est composée de plusieurs champs, chaque champ correspondant à une donnée.
Il existe de multiples structures de données, mais nous allons nous concentrer sur les plus connues :
- tableaux, listes chaînées et dictionnaires ;
- piles et files ;
- arbres binaires et graphs.
Ces structures sont parfois prévues « par défaut » par les langages de programmation.
Dans ces structures de données, vous pouvez créer, lire, modifier ou même supprimer des éléments. On parle alors de type d’opération que vous pouvez effectuer sur votre structure, il en existe bien d’autres.
Le type d’opération que nous souhaitons effectuer déterminera notre choix de structure, certaines étant plus efficaces pour la recherche, et d’autres pour la création ou la suppression de nouveaux éléments.
Commençons tout de suite par les tableaux !
Tableaux
Un tableau est une structure qui permet de mémoriser plusieurs données de type semblable ou différent. Autrement dit, cela ressemble en beaucoup de points aux tableaux de notre vie quotidienne.
Un tableau qui liste des objets éparpillés dans le labyrinthe :
| Indice | Valeur |
| 0 | Clé |
| 1 | Pied de biche |
| 2 | Épée |
Dans un tableau, chaque élément est associé à sa position dans la liste à l’aide d’un indice commençant à 0. Exactement comme dans une liste numérotée !
Cette position est appelée indice ou index. Attention, petite feinte : le premier élément de la liste est à l’index 0 et non 1 ! 😉
Selon le tableau ci-dessus, voici les points importants à considérer.
- L’index commence par 0.
- La taille du tableau est de 3, ce qui signifie qu’il peut stocker 3 éléments.
- Chaque élément est accessible via son indice. Par exemple, nous pouvons récupérer un élément à l’index 1 en tant que
Pied de biche.
Dans le pseudo-code, vous pouvez déclarer le tableau objets avec 5 cases par exemple, comme ceci :
Algorithme Tableau
Variable
objets[5] : TABLEAU CHAÎNE DE CARACTÈRES
Début
Fin
Pour expliciter :
- Vous devez tout d’abord donner le nom du tableau et ensuite mettre entre crochets la taille du tableau.
- Puis vous donnez le type du tableau précédé par les deux points.
- Il est aussi intéressant de donner le type de valeur contenu dans chaque case. Dans notre cas, j’ai spécifié que c’est un tableau de chaînes de caractères.
Avantages et inconvénients
D’une part, il est très facile de lire ou de modifier une donnée d’un tableau grâce à son index. Chaque donnée ayant un numéro, il vous suffit de le connaître, et le tour est joué.
D’autre part, dans plusieurs langages, la taille d’un tableau est fixe. Autrement dit, vous ne pouvez pas ajouter ou supprimer les données d’un tableau. Il vous faut en faire une copie intégrant vos ajouts ou vos suppressions. Ce n’est pas très pratique si vous devez changer fréquemment la taille de ce tableau.
Dans ce cas, vous préférerez d’autres structures de données, telles que les listes chaînées.
Listes chaînées
Une liste chaînée (singly-linked list, en anglais) est un ensemble de valeurs enregistrées dans des endroits différents de la mémoire. À la différence d’un tableau qui contient un nombre fixe d’éléments, la liste chaînée est très souple : vous pouvez ajouter ou supprimer des éléments à votre guise.
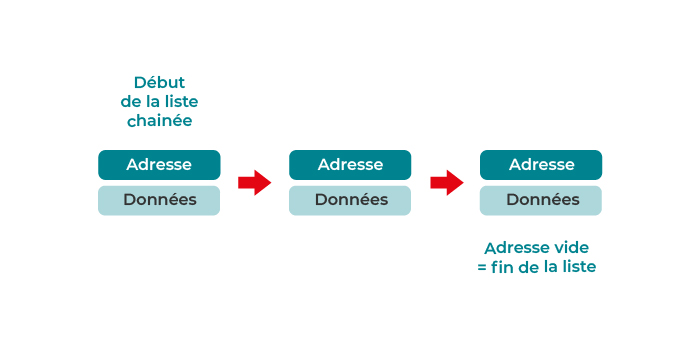
Ainsi, une liste chaînée est une structure de données linéaire qui comprend une série de nœuds connectés. Ici, chaque nœud stocke les données et l’adresse du nœud suivant ; le dernier élément de la liste aura une adresse vide.
À quoi ça sert, exactement ?
Dans un tableau, toutes les informations sont stockées de manière contiguë dans la mémoire de votre ordinateur. Cela permet d’accéder plus facilement aux données, mais il est, de fait, moins flexible. Une liste chaînée rend l’ajout et la suppression de valeurs plus faciles, mais l’accès à un élément plus long.
Avantages et inconvénients
Dans une liste chaînée, vous pouvez facilement ajouter un élément en début de liste et ensuite ajouter de nouveaux éléments en queue de liste. Mais c’est un peu plus compliqué, car il vous faut parcourir toute la liste avant de trouver un nœud dont l’adresse est vide. Concernant la recherche d’un élément, vous allez devoir parcourir la liste du début à la fin jusqu’à le trouver.
Parfois, vous êtes amené à associer deux éléments ensemble, mais actuellement, vous ne pouvez pas simplement associer un index et un élément avec les listes chaînées. Les tables de hachage vont vous permettre d’associer deux éléments de type quelconque. On parlera alors ici de l’association d’une clé et d’une valeur.
Tables de hachage
Une table de hachage est une structure de données qui vous permet d’associer une valeur à une clé et non plus à un indice. Cette clé peut être un mot ou un chiffre. Par exemple :
Un tableau qui stocke la correspondance entre le type du véhicule et le nombre de roues :
| Type du véhicule(clé) | Nombre de roues(valeur) |
| voiture | 4 |
| moto | 2 |
Les tables de hachage ne comportent pas d’ordre. Contrairement aux tableaux, vous ne pouvez pas retrouver un élément via sa position, mais uniquement via sa clé. Il s’agit d’une structure très commune et très pratique !
Opérations courantes
Pour retrouver une valeur, vous indiquez sa clé, contrairement à l’index dans un tableau.
Considérons que la table de hachage précédente est nommée roues ; pour récupérer le nombre de roues pour une voiture, nous devons écrire roues[“voiture”] .
Les tables de hachage sont très flexibles : vous pouvez ajouter ou supprimer des données rapidement.
Structures de données particulières
Mais que se passe-t-il si vous voulez accéder à vos données selon leur ordre d’arrivée ? Par exemple, si vous voulez trouver en premier la toute première information ajoutée ?
Laissez-moi vous présenter les piles et les files !
Qu’est-ce qu’une pile ?
Il s’agit d’une structure de données qui donne accès en priorité aux dernières données ajoutées. Ainsi, la dernière information ajoutée sera la première à en sortir.
Les piles sont ce que l’on appelle un traitement des données LIFO (Last In First Out, ou dans la langue de Molière : dernier ajouté, premier parti), très pratique lorsque nous aurons à utiliser en premier les dernières données ajoutées.
Pourquoi appeler cela une pile ? Car vous empilez les données comme vous le feriez avec des T-shirts dans votre armoire : la seconde vient « au-dessus » de la première.
Les piles sont très utilisées sur les plateformes de streaming musical comme Spotify ou Deezer par exemple. Lorsque vous demandez à la plateforme de lire une chanson à la suite, elle va ajouter cette dernière tout en haut de la liste « en attente de lecture ».
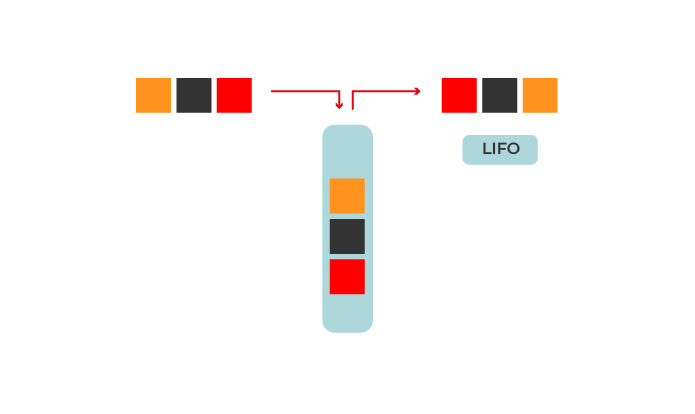
Les piles (de type LIFO) s’utilisent lorsque vous devez traiter en priorité les dernières données arrivées. Nous retrouvons ce système dans les placards de notre cuisine ou dans notre frigo : ce qui est mis en avant est ce que l’on va consommer le plus vite ! C’est également le cas dans le flux d’actualités de Facebook ou d’Instagram (la dernière information arrivée est la première que vous voyez), bien que ces plateformes utilisent également des algorithmes de curation pour montrer à l’utilisateur le contenu le plus adapté à ses besoins.
Mais que se passe-t-il si nous avons besoin d’accéder non pas aux dernières données ajoutées, mais aux premières ? C’est exactement ce qui se passe lorsque vous constituez une liste de musique. Vous ajoutez peu à peu les chansons qui seront lues dans le même ordre : les premières chansons ajoutées sont les premières lues. Impossible de réaliser cela avec une pile. C’est pourquoi les files existent !
Qu’est-ce qu’une file ?
Une file (queue, en anglais) est une structure de données dans laquelle on accède aux éléments suivant la règle du premier arrivé premier sorti, ou encore FIFO (First In First Out).
Elle suit la même logique que les files d’attente (au McDrive, à Pôle Emploi…) : plus vous arrivez tôt et plus vous partez tôt ! 😉
Prenons un exemple de notre vie courante. Vous vous rendez à la poste, car vous avez reçu un colis. Vous prenez un ticket qui vous indique votre place dans la file d’attente. Vous comparez alors ce numéro avec celui qui s’affiche, et vous avez une idée du nombre de personnes avant vous. Vous râlez : si seulement vous étiez arrivé plus tôt, vous auriez moins attendu ! Premier arrivé, premier servi (et premier parti !)…
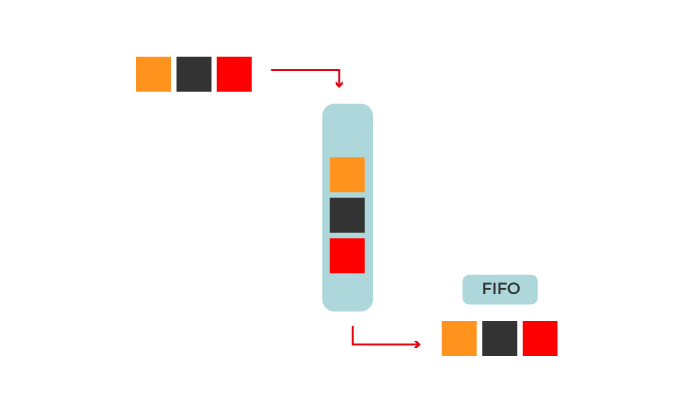
Les files (de type FIFO) s’utilisent lorsque vous devez traiter un flux de données par ordre d’arrivée. C’est le cas lorsque vous faites une to-do list (votre première action est celle que vous devez réaliser en priorité), ou que vous listez les bugs en attente de traitement.
À vous de jouer

Contexte
Voici notre nouveau labyrinthe :

Vous avez pu remarquer que dans certaines cases il y a des clés.
- Chaque clé a son petit nom, et vous en identifierez trois différentes dans ce labyrinthe.
- Le joueur possède un sac pour contenir l’ensemble des clés.
- Il va devoir toutes les ramasser avant de rejoindre la case Arrivée.
- S’il ne possède pas toutes les clés, il ne pourra pas ouvrir la porte pour sortir.
- Le sac sera ainsi assimilé à un tableau dans notre algorithme.
Vous utiliserez les deux fonctions suivantes pour insérer des données et récupérer la taille du tableau :
insérer(): cette fonction permet d’insérer une donnée dans le tableau, par exemple :nom_du_tableau.insérer(“Votre donnée”)taille(): cette fonction retourne le nombre de valeurs dans le tableau, par exemple :nom_du_tableau.taille()
Par ailleurs, vous allez pouvoir appeler la fonction déplacement pour gérer les déplacements du joueur.
Consigne
Vous devez tout d’abord créer une fonction qui permet d’insérer le nom de la clé dans le tableau une fois que le joueur passe dessus.
Ensuite vous allez devoir créer l’algorithme qui permet de gérer les déplacements, et qui vérifie si le joueur est passé sur un objet, et tout cela dans une boucle Tant que . Effectivement, la boucle s’arrêtera une fois que le joueur aura ramassé tous les objets et qu’il sera sur la case Arrivée.
Votre objectif :
- Construire une fonction
ramasserqui prend en paramètres le tableau et les coordonnées du joueur. Cette fonction va gérer l’insertion des noms des clés dans le tableau une fois que le joueur passe dessus.- Dans un premier temps, créer 6 variables pour assigner les coordonnées
xetyde chaque clé. - Dans un second temps, créer plusieurs structures conditionnelles pour gérer l’insertion des noms dans le tableau, en fonction des coordonnées du joueur et des objets.
- Dans un premier temps, créer 6 variables pour assigner les coordonnées
- Construire l’algorithme qui va appeler la fonction
déplacementetramasserdans une boucleTant que. N’oubliez pas de mettre la condition de boucle, et de créer l’ensemble des variables nécessaires.
Vérifiez votre travail
Voici les deux étapes à suivre pour obtenir le résultat à l’issue de l’exercice :
Première étape: construction de la fonction ramasser
Algorithme ramasser(clés, joueur_position_x, joueur_position_y)
Variable
volante_position_x ← 1 : ENTIER
volante_position_y ← 3 : ENTIER
passe-partout_position_x ← 5 : ENTIER
passe-partout_position_y ← 3 : ENTIER
celeste_position_x ← 0 : ENTIER
celeste_position_y ← 4 : ENTIER
Début
Si volante_position_x == joueur_position_x ET volante_position_y == joueur_position_y :
clés.insérer(“clé volante”)
Fin Si
Si passe-partout_position_x == joueur_position_x ET passe-partout_position_y == joueur_position_y :
clés.insérer(“clé passe-partout”)
Fin Si
Si celeste_position_x == joueur_position_x ET celeste_position_y == joueur_position_y :
clés.insérer(“clé celeste”)
Fin Si
Fin
Seconde étape: construction de l’algorithme qui appelle les fonctions ramasser et deplacement
Algorithme Labyrinthe
Variable
joueur_position_x ← 0 : ENTIER
joueur_position_y ← 0 : ENTIER
arrivée_position_x ← 5 : ENTIER
arrivée_position_y ← 5 : ENTIER
clés[3] : TABLEAU CHAÎNE DE CARACTÈRES
Début
Tant Que joueur_position_x != arrivée_position_x ET joueur_position_y != arrivée_position_y ET clés.taille() != 3:
déplacement(joueur_position_x, joueur_position_y)
ramasser(clés, joueur_position_x, joueur_position_y)
Fin Tant Que
Fin
En résumé
- Les structures de données sont utilisées pour stocker et organiser les données. C’est une façon d’organiser les données sur un ordinateur afin qu’elles puissent être consultées et mises à jour efficacement.
- Nous pouvons distinguer trois types de structures de données basiques :
- Dans un tableau, les éléments stockés sont disposés de manière contiguë. Chaque case d’un tableau est identifiée à l’aide de son index.
- Une liste chaînée est une séquence de structures de données, qui sont reliées entre elles par des liens.
- La table de hachage est une structure de données qui stocke les données de manière associative. Dans une table de hachage, chaque valeur de donnée a sa propre clé unique qui constitue l’identifiant de la case.
- Nous avons également deux autres types de structures de données plus complexes :
- Dans la structure de données en pile, les éléments sont stockés selon le principe LIFO. Autrement dit, le dernier élément stocké dans une pile sera le premier à sortir.
- La structure de données en file fonctionne selon le principe FIFO où le premier élément stocké dans la file sera le premier à sortir.
Dans le chapitre suivant, nous nous intéresserons à deux structures de données bien utiles pour retrouver des données selon les liens qu’elles entretiennent les unes avec les autres. À tout de suite !
Familiarisez-vous avec les arbres
Qu’est-ce qu’un arbre binaire ?
Vous souvenez-vous des listes chaînées ? Maintenant, imaginez que chaque nœud contienne deux adresses et non pas une. Si vous deviez le représenter par un schéma, cela ressemblerait étrangement à un arbre. C’est ce que nous appelons un arbre binaire.
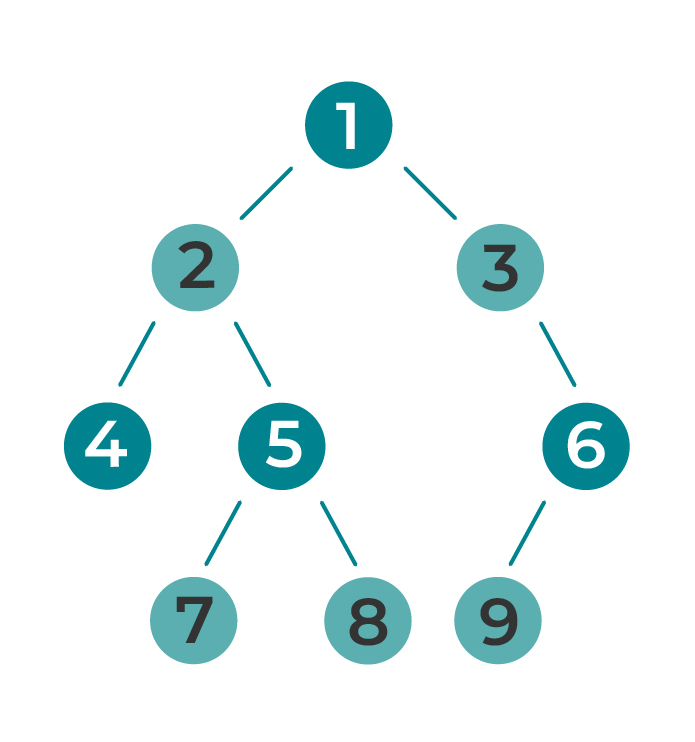
Comme dans un arbre généalogique, toutes les cellules sont des cellules filles, sauf une qui est la cellule mère. Si l’arbre n’est pas vide, une seule cellule n’a pas de cellule mère, et celle-ci est appelée racine de l’arbre. Toute cellule descend de la racine.
Les arbres binaires sont très largement utilisés en informatique car ils sont considérés comme les structures de données les plus simples et les plus efficaces à utiliser dans la plupart des systèmes logiciels. Ça paraît sûrement encore abstrait pour vous, mais ils sont utilisés par exemple dans :
- les jeux vidéo en 3D ;
- les routeurs Internet ;
- les bases de données ;
- les calculatrices.
Comme vous pouvez le voir, les arbres binaires sont omniprésents dans nos logiciels, il est donc important de comprendre leur fonctionnement.
Pourquoi l’appeler arbre binaire ?
Car chaque cellule mère a 0, 1 ou 2 cellules enfants qui elles-mêmes sont liées à d’autres cellules.
Dans la terminologie des arbres, les cellules sont appelées des nœuds ou des sommets. Un nœud n’ayant pas d’enfant s’appelle une feuille.
En d’autres termes, un arbre binaire est une structure analogue à une liste chaînée, sauf que chaque cellule possède jusqu’à deux suivantes. Par convention, on convient d’appeler fils gauche et fils droit les deux fils d’un nœud. Le fils gauche et le fils droit d’un nœud peuvent ne pas exister.
Parcours d’arbres binaires
Pour trouver une information dans un arbre binaire, il vous faut parcourir tous ses nœuds. Comment faire ? Le moyen le plus simple est de réaliser une fonction récursive.
Mais qu’est-ce qu’une fonction récursive ?
La récursivité est un processus qui prend tout son sens lorsque la résolution d’un problème se ramène à celle d’un problème plus petit. On parlera de récursivité lorsqu’une fonction s’appelle elle-même, en boucle, jusqu’à atteindre une condition d’arrêt.
Ne vous inquiétez pas, nous allons avoir un chapitre complet consacré à la récursivité dans la prochaine partie du cours. Vous avez déjà une idée de cette notion.
Il existe de nombreuses manières de parcourir un arbre selon l’ordre dans lequel vous souhaitez examiner les nœuds.
Nous n’allons pas entrer dans le détail des parcours, car ceux-ci mériteraient un cours à eux seuls ! Retenez simplement que les arbres sont très utiles pour trier des informations.
Qu’est-ce qu’un graphe ?
Un graphe est un ensemble de cellules reliées les unes aux autres non plus par un lien d’ascendance, comme dans le cas d’un arbre, mais par une relation. Visuellement, il s’agit d’un ensemble de nœuds ou de sommets reliés par des arêtes.
Un graphe peut représenter un réseau routier, un réseau de transport aérien, un réseau informatique et bien plus encore.
Les graphes sont souvent utilisés par des algorithmes dont le but est de trouver le plus court chemin entre un point A et un point B. Le service que nous connaissons tous qui utilise ce principe est Google Maps. Facebook utilise également les graphes pour trouver les amis de vos amis, et vous les présenter !
Sur Facebook, chaque personne du réseau est représentée par un cercle (appelé sommet). Vos amis sont reliés à vous par des lignes (appelées arcs). Les amis qui pourraient vous intéresser sont ceux qui sont reliés à vos amis par un arc, tout simplement !
Un chemin dans un graphe G est une suite de sommets tels que deux sommets consécutifs du chemin sont liés par un arc (orienté).

En résumé
- Un arbre binaire est une structure de données spéciale utilisée à des fins de stockage de données.
- Un arbre binaire présente les avantages à la fois d’un tableau ordonné et d’une liste chaînée.
- Un arbre binaire est composé de nœuds et d’enfants, chaque nœud pouvant avoir jusqu’à deux enfants.
- Un graphe est une représentation d’un ensemble d’objets où certaines paires d’objets sont reliées par des liens.
- Les objets interconnectés sont représentés par des points appelés sommets, et les liens qui relient les sommets sont appelés arêtes.
Vous avez appris plein de choses dans cette deuxième partie. Il est maintenant temps de tester vos connaissances à l’aide d’un petit quiz. Bonne chance !
Choisir le type et la structure de données adéquats
Compétences évaluées
- Choisir le type et la structure de données adéquats
Description
Dans ce quiz, vous allez aider un professeur à entrer les notes de ses 30 élèves à l’aide d’un algorithme.
Au fur et à mesure des questions, vous allez construire pas à pas cet algorithme en découpant un problème en petits sous-problèmes.
Vous vous souvenez de cette pratique ? Alors c’est parti et bon courage à vous !
- Question 1Le professeur souhaite entrer le nom de chaque étudiant dans son programme.Quel type de variable faut-il utiliser ?
- Un nombre entier
- Un booléen
- Une chaîne de caractères
- Question 2Le professeur va devoir entrer plusieurs informations concernant les étudiants. Pour cela, il a besoin :
- d’entrer le nom de l’étudiant ;
- d’enregistrer ensuite sa présence à l’examen ;
- de saisir une note comprise entre 0 et 20.
nom ← "" : CHAÎNE DE CARACTÈRES note ← 0 : NOMBRE DECIMAL est_présent ← "FAUX" : CHAÎNE DE CARACTÈRESnom ← "" : CHAÎNE DE CARACTÈRES note ← 0.0 : NOMBRE DECIMAL est_présent ← FAUX : BOOLÉENnom ← "" : CHAÎNE DE CARACTÈRES note ← 0 : NOMBRE ENTIER est_présent ← FAUX : BOOLÉEN
- Question 3À présent, nous voulons vérifier que le professeur n’a pas entré par erreur une note qui n’est pas comprise entre 0 et 20 inclus. Si c’est le cas, nous allons lui demander d’entrer à nouveau l’ensemble des informations à l’aide de la fonction
remplir_informations, et afficher le message suivant :La note n’est pas entre 0 et 20.Sinon, le programme afficheLa note est correcte.Cette fonctionremplir_informationscontient les instructions permettant au professeur d’entrer les informations pour un étudiant, et de les enregistrer dans les 3 variables précédentes. Quelle structure conditionnelle permet de gérer cette erreur de frappe ?Si note >= 0.0 OU note <= 20.0 : Afficher "La note est correcte." Sinon Afficher " La note n’est pas entre 0 et 20." remplir_informations()Si note <= 0.0 ET note >= 20.0 : Afficher "La note est correcte." Sinon Afficher " La note n’est pas entre 0 et 20." remplir_informations()Si note >= 0.0 ET note <= 20.0 : Afficher "La note est correcte." Sinon Afficher " La note n’est pas entre 0 et 20." remplir_informations()
- Question 4Précédemment, vous avez pu protéger la saisie de la note de l’élève grâce à notre structure conditionnelle. Effectivement, en cas d’erreur, le programme va demander une nouvelle fois d’entrer les informations et la note. Mais que se passe-t-il s’il se trompe encore ? Il ne se passe rien malheureusement, cette dernière note sera prise en compte comme note finale. Il nous faut donc une solution plus adaptée.Nous allons cette fois utiliser une boucle !Quelle boucle permet de remplacer la structure conditionnelle précédente pour gérer la saisie de la note ?
Tant que note < 0.0 OU note > 20.0 : Afficher " La note n’est pas entre 0 et 20." remplir_informations()Pour i allant de 1 jusqu’à 30 : Afficher " La note n’est pas entre 0 et 20." remplir_informations()Tant que note >= 0.0 OU note <= 20.0 : Afficher " La note n’est pas entre 0 et 20." remplir_informations()
- Question 5Vous avez pu terminer toutes les fonctions qui permettent de gérer les informations d’un étudiant. Mais il est maintenant temps de s’occuper des autres élèves. En effet, vous devez enregistrer les notes des 30 étudiants au même endroit grâce à un autre type de données : le tableau !Quelle déclaration de variable correspond à notre tableau ?
notes ← 0 : TABLEAU DE NOMBRES DECIMAUXnotes[30] : TABLEAU DE NOMBRES DECIMAUXnotes ← 30.0: TABLEAU DE NOMBRES DECIMAUX
- Question 6Vous avez précédemment créé un tableau qui permet de contenir 30 nombres entiers. Il va maintenant falloir le remplir à l’aide d’une boucle. En effet, chaque case contiendra la note d’un élève.Quelle boucle est la plus adaptée pour inscrire les 30 notes d’élèves ?
Pour i allant de 0 jusqu’à 29 : Notes[i] ← notei ← 0 Tant que i < 30 : Notes[i] ← note i ← i + 1Pour i allant de 1 jusqu’à 30 : Notes[i] ← note
- Question 7Mais nous avons oublié quelque chose non ? Comment savoir à qui appartient la note dans une case de notre tableau ?Le professeur souhaite finalement associer un nom à une note.Quel type de structure de données permet d’associer un nom et la note ?
- Une pile
- Une file
- Une table de hachage
- Question 8Finalement, le professeur a encore changé d’avis, il aimerait ordonner ses données sous la forme de nœuds interconnectés. Il souhaite avoir des nœuds liés au maximum avec 2 autres nœuds.Quel type de structure de données pourrait-il choisir ?
- Arbre binaire
- Arbre quelconque
- Graphe
Triez des informations
Nous avons vu que les algorithmes nous permettaient de résoudre des problèmes plus ou moins complexes. Un des problèmes les plus répandus consiste à trier les informations. Cela vous semble facile à faire ? Et pourtant ! Il ne nous faut pas seulement trier les informations, mais également trouver la manière la plus efficace de le faire.
Trier une suite de 10 nombres du plus petit au plus grand n’est effectivement pas très long. Mais qu’en est-il lorsque nous avons 100 000 nombres à trier ? Que se passe-t-il lorsque vous vous appelez Google et que vous devez trier plusieurs centaines de gigaoctets d’e-mails ?
Les algorithmes de tri sont l’essence même de l’algorithmique. En effet, nous souhaitons souvent réorganiser des données pour les manipuler autrement. Il est donc essentiel d’en savoir un peu plus.
Découvrons ensemble un des algorithmes de tri les plus connus : le tri à bulles !
Le tri à bulles
Cet algorithme progresse dans une liste d’éléments. Il compare les données deux à deux et les échange si la première valeur est plus élevée que la seconde. Il fait cela pour toutes les paires d’éléments dans une liste, puis recommence au début jusqu’à ce que toutes les paires soient dans le bon ordre.
Faisons une démonstration avec des livres ! Nous avons tous eu un jour ou l’autre à trier notre bibliothèque, que ce soit par ordre alphabétique, par auteur ou par hauteur. Pour cette démonstration, disons que nous trions les livres par hauteur.
Nous saisissons le premier livre et le comparons au suivant. S’il est plus grand, nous les échangeons. Sinon, nous les laissons ainsi.
Quand nous avons fini de parcourir tous les livres une première fois, le plus grand se trouve bien à la fin. Nous pouvons alors recommencer un tour de boucle pour placer l’élément suivant.
Et ainsi de suite jusqu’à ce que la bibliothèque soit triée !
Pourquoi ce nom « tri à bulles » ? Tout simplement parce que la plus grande donnée remonte peu à peu à la fin de la liste, exactement comme des bulles de savon.
Comment l’écririons-nous en pseudo-code ?
Nous commençons par écrire une fonction qui va parcourir tous les livres, un à un. Vous connaissez déjà cette structure : il s’agit d’une boucle ! Nous allons donc faire 10 tours, puisque nous allons parcourir une liste de 10 livres, mais, pour changer, de la dernière case à la première.
Algorithme Tri_a_bulle(tableau)
taille ← Taille du tableau
Pour i allant de taille - 1 jusqu’à 1 :
…
Fin Pour
Fin
Quand nous sommes dans la boucle, nous intervertissons les livres si le second est plus grand que le premier. Nous pouvons donc utiliser les structures conditionnelles que nous avons déjà vues.
Algorithme Tri_a_bulle(tableau)
taille ← Taille du tableau
Pour i allant de taille - 1 jusqu’à 1 :
Si tableau[i] < tableau[i-1] :
echanger(tableau[i], tableau[i-1])
Fin Si
Fin Pour
Fin
Ceci est déjà très bien, mais ce n’est pas suffisant. Actuellement, chaque item a bougé d’une place, mais n’est pas vraiment remonté jusqu’à la fin. Alors, comment faire ?
Si nous réfléchissons bien, il faut faire un nombre de boucles correspondant au nombre d’items restant à trier dans la liste au carré.
Prenons l’exemple du premier livre. S’il s’agit du plus grand, notre algorithme devra effectuer 9 tours de boucle afin de le positionner à la fin. Mais une fois que le livre est en place, il sait qu’il n’a pas à aller jusqu’à la fin. Il peut donc effectuer 8 tours de boucle, puis 7, puis 6 et ainsi de suite jusqu’à 1.
En pseudo-code, nous allons le représenter ainsi :
Algorithme Tri_a_bulle(tableau)
taille ← Taille du tableau
Pour i allant de taille - 1 jusqu’à 1 :
Pour j allant de 0 jusqu’à i - 1
Si tableau[j+1] < tableau[j] :
echanger(tableau[j+1], tableau[j])
Fin Si
Fin Pour
Fin Pour
Fin
Autres algorithmes de tri
Le tri à bulles est le plus connu de tous, mais pas le plus efficace. D’ailleurs, nous-mêmes, lorsque nous devons trier des livres, nous ne comparons pas deux livres et ainsi de suite. Nous utilisons d’autres algorithmes.
Si nous avons une grande bibliothèque, nous pouvons décider de la diviser en plusieurs unités plus petites afin de les trier séparément, et ensuite de les fusionner. Ou bien, nous nous disons : je mets les livres les plus grands et les plus petits au début, en même temps.
Bref, nous avons chacun notre stratégie. Il existe trop d’algorithmes de tri différents pour tous les expliquer ici. Je vous propose un tableau résumant les types de tri les plus utilisés :
| Type de tri | Description |
| Tri par insertion | Le tri par insertion considère chaque élément du tableau, et l’insère à la bonne place parmi les éléments déjà triés. |
| Tri par sélection | Le tri par sélection est un algorithme de tri qui sélectionne à chaque itération le plus petit élément d’une liste non triée, et place cet élément au début de la liste non triée. |
| Tri par tas | Le tri par tas débute par la construction d’un tas sur le tableau d’entrée. Comme l’élément maximum du tableau est stocké à la racine, on peut le placer dans sa position finale correcte en l’échangeant avec le dernier élément du tableau. |
| Tri par fusion | Le tri par fusion fonctionne sur le principe de diviser pour mieux régner. Le tri par fusion décompose à plusieurs reprises une liste en plusieurs sous-listes jusqu’à ce que chaque sous-liste se compose d’un seul élément, et fusionne ces sous-listes de manière à obtenir une liste triée. |
Un tas est une structure de données qui peut être représentée par un arbre binaire, dans lequel tous les nœuds de l’arbre sont dans un ordre spécifique.
Je vous conseille néanmoins de regarder cette liste non exhaustive des différents tris proposés sur cette page Wikipédia, et d’en lire quelques définitions afin de mieux les comprendre.
À vous de jouer

Contexte
Rappelez-vous que la porte à l’arrivée du labyrinthe est verrouillée à l’aide de 3 clés. Ces clés sont numérotées de 1 à 3. La clé qui a le numéro 1 correspond au trou de serrure le plus haut sur la porte, la clé qui a le numéro 2 à la suivante en dessous, et ainsi de suite. Pour éviter de perdre du temps à l’arrivée, il serait intéressant de trier le sac à l’aide des numéros des clés par ordre croissant, afin de les sortir dans l’ordre.
Consigne
Vous devez écrire le pseudo-code d’un algorithme de tri par insertion. Un tri par insertion compare les valeurs deux à deux, en commençant par la deuxième valeur de la liste. Si cette valeur est supérieure à la valeur située à sa gauche, aucune modification n’est apportée. Sinon, cette valeur est déplacée à plusieurs reprises vers la gauche jusqu’à ce qu’elle rencontre une valeur inférieure à elle.
Votre objectif :
- Enregistrer la taille du tableau dans une variable
N. - Parcourir le tableau de la deuxième case à la fin du tableau.
- Enregistrer temporairement l’élément courant de votre itération.
- Comparer cet élément avec tous les éléments de la sous-liste triée.
- Décaler tous les éléments de la sous-liste supérieurs à la valeur à trier.
- Insérer la valeur temporaire.
- Répéter jusqu’à ce que la liste soit triée.
Vérifiez votre travail
Voici le résultat à obtenir à l’issue de l’exercice :
Algorithme Tri_par_insertion(tableau)
N ← Taille du tableau
Pour i allant de 1 jusqu’à N - 1 :
x ← tableau[i]
j ← i
Tant que j > 0 ET tableau[j-1] > x :
tableau[j] ← tableau[j-1]
j ← j - 1
Fin Tant que
tableau[j] ← x
Fin Pour
Fin
En résumé
- Le tri des données est une tâche importante et largement utilisée lors du développement de logiciels.
- Il existe différents types de tri, tels que le tri à bulles, le tri par sélection, le tri par insertion et bien d’autres.
- Tous les algorithmes ne sont pas efficaces pour un même problème, il faudra donc choisir l’algorithme de tri adapté au problème.
Je vous ai expliqué précédemment que tous les algorithmes ne sont pas adaptés à toutes les situations. Mais pourquoi ? En fonction du problème, le temps peut être plus ou moins long. On parle alors de la complexité de l’algorithme. Nous allons voir dans le prochain chapitre comment la calculer.
Calculez la complexité algorithmique
Vous avez pu voir qu’un algorithme peut être créé de mille et une façons. Mais comment pouvez-vous savoir si votre algorithme est plus efficace qu’un autre, ou même savoir s’il est performant ?
Pour cela, vous allez devoir analyser la complexité de votre algorithme. Ainsi, vous pourrez conclure que cette complexité est convenable, ou la comparer avec d’autres algorithmes.
Qu’est-ce que la complexité algorithmique ?
La complexité algorithmique est un concept très important qui permet de comparer les algorithmes afin de trouver celui qui est le plus efficace. Il existe une notation standard qui s’appelle big O et qui permet de mesurer la performance d’un algorithme. Vous verrez, au fur et à mesure des explications, la méthode de calcul.
Avant d’entrer dans le détail de son calcul, laissez-moi vous conter une petite histoire.
La complexité exponentielle
Nous sommes dans le Midi, au cœur d’une belle forêt, et nous nous promenons paisiblement. Soudain, un éclat de lumière attire votre regard. Vous vous approchez. Quelle n’est pas votre surprise lorsque vous apercevez un coffre qui semble être sorti tout droit d’un bateau pirate !
Vous soulevez le coffre et tombez nez à nez avec un cadenas à trois chiffres, en fonte, bien décidé à ne pas vous laisser accéder au trésor tant escompté. Quand bien même ! Nous décidons de relever le défi et de tester rapidement, une à une, toutes les combinaisons.
Plutôt que de les tester dans le désordre, car il serait impossible de se souvenir de toutes les tentatives, nous réfléchissons à différentes stratégies. L’une d’elles consiste à essayer le nombre le plus petit (000) puis le nombre suivant (001) et ainsi de suite jusqu’à atteindre 999. En effet, nous calculons que cette stratégie nous prendra, dans le pire des cas, 30 minutes.
Effectivement, quelques minutes plus tard, le cadenas s’ouvre. Hourra ! Le code était 123. Facile ! Notre stratégie était efficace et nous nous félicitons d’être si intelligents.
Voyons maintenant comment décrire ce problème avec le pseudo-code :
Algorithme cadenas_3_chiffres
Début
Pour i allant de 0 jusqu’à 9 :
Pour j allant de 0 jusqu’à 9 :
Pour k allant de 0 jusqu’à 9 :
Si code == combinaison :
Arrêter les boucles
Fin Si
Fin Pour
Fin Pour
Fin Pour
Fin
Nous avons dans cet algorithme 3 boucles allant de 0 à 9 donc 10 x 10 x 10 itérations, soit 10^3 itérations. Avec la notation Big O, on dira que la complexité temporelle de cet algorithme est de O(103)�(103) .
Nous ouvrons le coffre… pour en découvrir un second, plus petit, comportant un cadenas à 4 chiffres. Tristesse.
Forts de notre premier succès, nous nous basons sur le même algorithme pour trouver le code. Au bout d’une heure et demie, las, nous abandonnons l’idée. C’est le plus raisonnable : tester toutes les combinaisons possibles aurait pris plus de 5 heures.
Nous reprenons notre marche, le petit coffre sous le bras, et partons dans un grand débat : comment en est-on arrivés là ? Comment le temps de calcul peut-il passer de 30 minutes à 5 heures en ajoutant un simple chiffre ? Le secret, c’est la complexité de notre algorithme.
Au risque de ne pas vous surprendre, plus il y a de chiffres dans le code, plus il sera long à trouver. Mais plus long comment ?
Si le code a 3 chiffres, il faut tester 1 000 combinaisons (eh oui, tous les nombres entre 000 et 999). En revanche, s’il en a 4, il faut en tester 10 000. S’il en avait eu 5, il aurait fallu en tester 100 000, et ainsi de suite. Nous nous apercevons donc que notre algorithme d’ouverture de coffre dépend du nombre de chiffres du code.
Plus précisément, le temps mis à l’ouvrir est multiplié par 10 à chaque fois que l’on ajoute un chiffre : 10 pour un code à 1 chiffre, 100 (10 x 10) pour un code à 2 chiffres, 1 000 (10 x 10 x 10) pour un code à trois chiffres, et ainsi de suite.
Si l’on note n le nombre de chiffres de notre cadenas, le temps de calcul est donc 10n10� ; ainsi, à l’aide de la notion big O, nous pouvons noter que la complexité temporelle de notre algorithme est de O( 10n10�).
On dit alors que la complexité est exponentielle. Très vite, nous nous sommes rendu compte que notre algorithme était impossible à réaliser, car il devenait trop long.
La complexité linéaire
Après avoir disserté sur ce sujet, nous avons soudain une idée : et si nous arrêtions de calculer et faisions appel à Bill, notre cousin, celui qui trempe dans des affaires louches ? Il nous a raconté un jour qu’il savait « écouter les cadenas« . Sa technique est simple : il tourne la molette du premier chiffre jusqu’à entendre un « clic« . Il sait alors que le chiffre est bon et passe au suivant. Il peut donc trouver les bons chiffres un par un, sans avoir à se soucier des autres.
Évidemment, le jour où il vous a exposé sa théorie vous avez bien ri. À présent, vous êtes dubitatif : vous avez passé deux heures à essayer d’ouvrir des coffres de pirates, alors bon, pourquoi ne pas tenter ?
Au bout de deux minutes, le cadenas à 4 chiffres est ouvert. Youpi ! À présent, nous ouvrons le coffre et en découvrons le contenu. Il est à la hauteur de nos efforts !
Mais comment peut-on aller si vite, alors que nous avons exactement le même nombre de chiffres sur le cadenas ?
C’est très simple ! Afin de trouver le premier chiffre du code, Bill tente 10 combinaisons. Quand il l’a trouvé, il passe au suivant et teste de nouveau 10 combinaisons. Et ainsi de suite pour chaque chiffre !
Il n’aura donc à tester que 40 combinaisons (10 + 10 + 10 + 10, soit 10 x 4) pour ce cadenas à quatre chiffres (ce qui est mieux que les 10 000 combinaisons que nous nous apprêtions à essayer…).
Voyons maintenant comment décrire cette nouvelle solution avec le pseudo-code :
Algorithme cadenas_4_chiffres
Variable
chiffre_1 ← 0 : ENTIER
chiffre_2 ← 0 : ENTIER
chiffre_3 ← 0 : ENTIER
chiffre_4 ← 0 : ENTIER
Début
Pour i allant de 0 jusqu’à 9 :
Si entendre un “clic” :
chiffre_1 ← i
Fin Si
Fin Pour
Pour j allant de 0 jusqu’à 9 :
Si entendre un “clic” :
chiffre_2 ← j
Fin Si
Fin Pour
Pour k allant de 0 jusqu’à 9 :
Si entendre un “clic” :
chiffre_3 ← k
Fin Si
Fin Pour
Pour m allant de 0 jusqu’à 9 :
Si entendre un “clic” :
chiffre_4 ← m
Fin Si
Fin Pour
Fin
Si l’on y regarde de plus près, Bill teste 10 nouvelles combinaisons pour chaque nouveau chiffre du cadenas. Autrement dit, si n est le nombre de chiffres, il teste 10 x n combinaisons. Ainsi avec la notation big O, nous pouvons dire que cet algorithme a une complexité de O(10xn)�(10��) . La « complexité » de son algorithme était bien meilleure que la nôtre.
Nous appelons cela une complexité linéaire. Pourquoi ? Car elle augmente proportionnellement au nombre de chiffres.
La complexité en temps constant
Tout contents, nous allons rendre visite à Bill pour lui montrer le cadenas et crâner un peu. Pour sûr, il sera impressionné !
Bill vous adresse un regard circonspect. « Vous voulez vous amuser ? Voilà de quoi faire ! », vous dit-il, sortant d’un placard un cadenas à 500 chiffres qui manque de faire écrouler la table de la salle à manger. « Il faut tester 5 000 combinaisons, ce qui prendra environ 3 heures. Enfin… Si vous êtes rapides. »
Mince, nous nous retrouvons dans le même problème que tout à l’heure. Aussi efficace que soit sa technique, le nombre de chiffres du cadenas est trop important. Autrement dit, la taille des données du problème excède la capacité de son algorithme.
C’est là que passe Jack, votre neveu. Il rigole, prend une pierre et tape sur le cadenas. Paf ! Ce dernier s’ouvre d’un coup sec. Effectivement… Cela paraît si simple, maintenant que l’on y pense…
Si l’on s’y attarde de plus près, son algorithme est sacrément efficace ! Quel que soit le nombre de chiffres, il prend toujours le même temps. Balèze !
Nous parlons alors de complexité en temps constant. On note ce type de complexité avec la notation big O, O(1)�(1) .
La complexité temporelle
Si nous comparons nos différents algorithmes, nous nous rendons compte que nous avons surtout pris en compte le facteur temps : notre première solution nous a pris 30 minutes quand celle de Jack ne demande qu’une seconde.
Il en sera de même pour chaque algorithme, que ce soit le tri d’une liste, la décomposition en facteurs premiers ou encore la recherche du cours le plus suivi sur OpenClassrooms. Nous parlons alors de complexité temporelle.
Quel est l’intérêt, me direz-vous ? Cela nous permet de savoir à l’avance si un algorithme ne se terminera jamais. Bien pratique !
Si nous avions utilisé notre algorithme naïf pour ouvrir le cadenas à 500 chiffres, un milliard d’années ne nous auraient pas suffi à trouver la bonne combinaison. Inutile de dire que nous serions morts, réincarnés et re-morts avant de pouvoir profiter du contenu derrière le cadenas.
Internet nous offre une autre application très importante de ce concept. Imaginons un site de restauration à emporter. Que se passe-t-il lorsque vous cherchez tous les restaurants asiatiques à 1 km de chez vous, ouverts jusqu’à 23 heures et qui livrent à domicile ? L’algorithme va tout faire pour trouver le résultat de votre recherche. Malgré cela, vous n’avez pas envie d’attendre 3 heures. Vous souhaitez que le site affiche la page de résultats en une seconde ou deux, pas plus. Il est donc primordial de trouver l’algorithme le plus efficace qui soit.
La complexité spatiale
Le dernier point à connaître concerne le stockage des données. Lorsque nous réalisons un algorithme en informatique, les informations sont stockées sur la mémoire de l’ordinateur. Or, vous l’aurez deviné, cette mémoire n’est pas infinie. Si nous ne faisons pas attention, un algorithme peut vite occuper tout l’espace libre d’un ordinateur, et le faire planter.
On parle ici de complexité spatiale (en espace). Les notations big O sont exactement les mêmes que pour la complexité temporelle.
Imaginez un algorithme où l’utilisateur doive entrer n éléments et les enregistrer dans un tableau. Dans ce cas, la complexité spatiale se notera avec la notation big O, O(n)�(�) . Car le tableau contiendra finalement n éléments. Et si à l’aide des mêmes n éléments, l’algorithme construit deux tableaux de n éléments, cette fois la complexité spatiale sera de O(2n)�(2�) , car l’algorithme crée 2 tableaux de n cases.
À vous de jouer

Contexte
Tout au long de ce cours, vous avez pu créer des algorithmes pour le labyrinthe. Nous allons en prendre quelques-uns et calculer la complexité temporelle et spatiale de ceux-ci.
Consigne
Nous allons calculé la complexité temporelle et spatiale de 3 algorithmes.
- Nous avons tout d’abord l’algorithme de déplacement suivant :
Algorithme déplacement(position_x , position_y)
Variable
sens ← “” : CHAÎNE DE CARACTÈRES
Début
sens ← entrer()
Si sens == “Haut” OU sens == “Bas” OU sens == “Droite” OU sens == “Gauche” :
Si sens == “Haut” :
position_y = position_y + 1
Fin Si
Si sens == “Bas” :
position_y = position_y - 1
Fin Si
Si sens == “Droite” :
position_x = position_x + 1
Fin Si
Si sens == “Gauche” :
position_x = position_x - 1
Fin Si
Sinon
afficher “L’entrée n’est pas correcte”
Fin Si
Fin
- Nous avons ensuite l’algorithme suivant qui permet de ramasser un nombre n de clés dans le labyrinthe :
Algorithme ramasser
Variable
joueur_position_x ← 0 : ENTIER
joueur_position_y ← 0 : ENTIER
arrivée_position_x ← 5 : ENTIER
arrivée_position_y ← 5 : ENTIER
clés[n] : TABLEAU CHAÎNE DE CARACTÈRES
déplacement ← 0 : ENTIER
max_déplacement ← 30n : ENTIER
Début
Tant Que joueur_position_x != arrivée_position_x ET joueur_position_y != arrivée_position_y ET clés.taille() != n ET déplacement < max_déplacement :
déplacement(joueur_position_x, joueur_position_y)
ramasser(clés, joueur_position_x, joueur_position_y)
Fin Tant Que
Fin
- Pour terminer, nous avons l’algorithme de tri suivant :
Algorithme Tri(tableau)
taille ← Taille du tableau
Pour i allant de 0 jusqu’à taille - 1 :
Pour j allant de 0 jusqu’à taille - 1 - 1 :
Si tableau[j+1] < tableau[j] :
echanger(tableau[j+1], tableau[j])
Fin Si
Fin Pour
Fin Pour
Fin
Votre objectif :
- Mesurer la complexité temporelle et spatiale des 3 algorithmes :
- déplacement ;
- ramassage ;
- tri.
Vérifiez votre travail
Voici le résultat à obtenir à l’issue de l’exercice :
- La fonction
déplacement:- complexité temporelle : O(1)�(1) .
La complexité est constante, il n’y a aucune boucle ni aucune fonction récursive. - complexité spatiale : O(1)�(1) .
La mémoire n’est pas affectée par cet algorithme.
- complexité temporelle : O(1)�(1) .
- La fonction
ramasser:- complexité temporelle : O(30n)�(30�) .
Au pire des cas, la boucle va itérer 30 x n fois. - complexité spatiale : O(n)�(�) .
La complexité est linéaire, le tableau aura au maximum n cases.
- complexité temporelle : O(30n)�(30�) .
- La fonction
tri:- complexité temporelle : O(n2)�(�2) .
Il y a deux boucles imbriquées qui itèrent n fois, donc nous avons au maximum n x n itérations. - complexité spatiale : O(1)�(1) .
La mémoire n’est pas affectée par cet algorithme, car la taille du tableau ne change pas.
- complexité temporelle : O(n2)�(�2) .
En résumé
- La complexité d’un algorithme est une mesure de la quantité de temps et/ou d’espace requise par un algorithme.
- La complexité temporelle est le temps nécessaire à l’exécution d’un algorithme, en fonction de la longueur des données en entrée.
- La complexité spatiale mesure la quantité totale de mémoire dont un algorithme ou une opération a besoin pour s’exécuter en fonction de la longueur de données en entrée.
- La notation big O est une notation standard pour décrire la complexité d’un algorithme.
C’est bientôt terminé, il ne reste plus qu’un chapitre. Je vous propose de voir un concept assez avancé de l’informatique, qu’on appelle la récursivité. Je vous attends avec impatience dans ce dernier chapitre.
Voyez le monde autrement avec la récursivité
En programmation, nous avons vu que nous pouvions utiliser des boucles pour répéter une opération. Nous les appelons des boucles itératives. Laissez-moi vous présenter un nouveau concept : la récursivité.
Il s’agit d’un concept un peu spécial. Avez-vous déjà rêvé que vous rêviez ? Vous y êtes ! Nous allons parler de concepts qui s’appellent eux-mêmes. C’est parti !
Qu’est-ce que la récursivité ?
La récursivité est un concept qui fait référence à lui-même dans son fonctionnement.
Les poupées russes sont une excellente métaphore de la récursivité. Si vous n’avez jamais joué avec des poupées russes, elles sont exactement ce à quoi elles ressemblent. Chaque poupée est la même sauf pour sa taille ; elles s’ouvrent chacune, et la poupée à l’intérieur est de plus en plus petite jusqu’à ce que vous arriviez au plus petit enfant, qui ne s’ouvre pas. Lorsque vous atteignez le plus petit enfant, vous inversez le processus en fermant chaque poupée une par une dans l’ordre inverse.
Par ailleurs, nous utilisons tous les jours la récursivité lorsque nous définissons des mots ! En effet, nous utilisons des mots pour en définir d’autres, eux-mêmes étant définis par d’autres mots !
La récursivité en programmation
En programmation, il s’agit d’une fonction qui fait référence à elle-même. Deux fonctions peuvent s’appeler l’une l’autre, on parle alors de récursivité croisée.
Essayons de retranscrire l’exemple des poupées russes à l’aide d’une fonction récursive. Nous allons alors compter le nombre de poupées à l’aide d’une fonction récursive.
Nous devons tout d’abord créer la fonction qui prend en paramètre une poupée, qu’elle contienne ou non une autre poupée :
Algorithme nombre_de_poupées(poupée)
Début
Fin
Nous pouvons maintenant construire le corps de la fonction. Si la poupée en paramètre contient une autre poupée, nous retournons 1 pour compter cette poupée, et nous appelons de manière récursive la même fonction pour vérifier si l’autre poupée contient aussi une autre poupée.
Algorithme nombre_de_poupées(poupée)
Début
Si poupée contient une autre poupée :
Retourner 1 + nombre_de_poupées(poupée à l’intérieur)
Fin Si
Fin
Pour terminer, nous devons trouver un moyen d’arrêter cette fonction récursive, sinon nous aurons une boucle infinie. Ainsi, si la poupée ne contient pas de poupée, nous allons retourner 1, simplement pour comptabiliser cette poupée.
Nous avons donc cette fonction finale :
Algorithme nombre_de_poupées(poupée)
Début
Si poupée contient une autre poupée :
Retourner 1 + nombre_de_poupées(poupée à l’intérieur)
Sinon
Retourner 1
Fin Si
Fin
Comme pour les boucles, il faut toujours penser à une condition qui permette d’arrêter les appels récursifs.
La suite de Fibonacci
Avez-vous déjà passé un entretien d’embauche technique pour travailler en tant que développeur·se, par exemple ? Si oui, la suite de Fibonacci vous parlera certainement ! Il s’agit d’un des problèmes les plus couramment posés en entretien.
La suite de Fibonacci est une liste de nombres entiers. Elle commence généralement par les nombres 0 et 1 (parfois 1 et 1). On appelle un nombre de cette liste un terme. Chaque terme est la somme des deux termes qui le précèdent.
Par exemple, si la suite de Fibonacci débute ainsi : 0, 1, 1, 2, 3, 5, 8, 13, 21, etc., vous voyez que 0 + 1 donne 1, que 1 + 2 donne 3, que 3 + 5 donne 8, et ainsi de suite.
Il existe plusieurs manières de résoudre le problème lié à la suite de Fibonacci. Prenez quelques minutes pour réfléchir aux différents algorithmes que vous pourriez inventer.
Pour résoudre ce problème, nous allons utiliser une méthode récursive et une méthode itérative, afin que vous puissiez comparer les deux possibilités !
La méthode par algorithme récursif naïf
Un algorithme naïf désigne un algorithme « simple », très proche de notre pensée quotidienne. Concrètement, il s’agit de la première manière qui vous vient à l’esprit pour résoudre un problème.
Dans notre cas, nous pouvons dire :
Algorithme fibonacci(n)
Début
Si n <= 1:
Retourner 1
Sinon
Retourner fibonacci(n - 1) + fibonacci(n - 2)
Fin Si
Fin
Si on appelle la fonction fibonacci avec le paramètre 3 fibonacci(3) , la fonction renverra 3. Mais pourquoi ?
fibonacci(3): appelle les fonctionsfibonacci(2)etfibonacci(1):fibonacci(1): cette fonction s’arrête et renvoie 1.fibonacci(0): cette fonction s’arrête et renvoie 1.- Donc
fibonacci(2)renvoie 1 + 1.
fibonacci(2): appelle les fonctionsfibonacci(1)etfibonacci(0).fibonacci(1): cette fonction s’arrête et renvoie 1.
- Finalement on additionne ce que retournent
fibonacci(2)etfibonacci(1), soit 2 + 1.
Donc fibonacci(3) = 3.
Le problème dans ce cas est que nous consommons beaucoup de mémoire. En effet, le calcul est exponentiel : il demande deux calculs différents pour se calculer lui-même.
Quand nous calculons la valeur d’un nombre, nous réalisons les trois opérations suivantes :
- calcule fibonacci(n-1) [qui lui-même va calculer fibonacci(n-1) et ainsi de suite jusqu’à arriver au chiffre 1] et garde la valeur en mémoire ;
- calcule fibonacci(n-2) [fais-en de même à chaque fois jusqu’à arriver à 1] et garde la valeur en mémoire ;
- enfin, ajoute les deux précédentes valeurs.
Nous voyons par conséquent que ce calcul est exponentiel : chaque nouveau nombre demande deux fois plus de mémoire que son précédent. Sa complexité est de O(2^n).
Peut-on trouver une manière moins consommatrice de le calculer ?
Nous avons sans doute une solution toute trouvée avec un algorithme linéaire !
La méthode par algorithme linéaire
Et si vous calculiez deux valeurs consécutives à la suite ? Cela serait mieux, non ?
Nous pouvons ainsi écrire la fonction suivante :
Algorithme fibonacci(n)
Variable
a ← 0 : ENTIER
b ← 1 : ENTIER
c ← 0 : ENTIER
Début
Pour i allant de 1 jusqu’à n:
c ← a + b
a ← b
b ← c
Retourner b
Fin
À présent, chaque nouveau nombre n’a plus besoin de deux niveaux d’opération pour le générer, mais d’un seul. Il est donc linéaire et sa complexité est de O(n).
Nous voyons ici que, dans bien des cas, nous préférerons la version itérative, car elle est moins consommatrice en mémoire. La récursivité n’est pas la solution à tous les problèmes.
Voici les étapes importantes pour programmer une fonction récursive :
- Décomposer le problème en un ou plusieurs sous-problèmes du même type. On résout les sous-problèmes par des appels récursifs.
- Les sous-problèmes doivent être de taille plus petite que le problème initial.
- Enfin, la décomposition doit en fin de compte conduire à un élémentaire qui, lui, n’est pas décomposé en sous-problèmes (c’est la condition d’arrêt).
Vous vous rappelez quand nous avons décomposé l’appel de chaque fonction récursivement pour le cas de la suite de Fibonacci ? Nous avons pu identifier l’ordre d’appel de chaque fonction pour identifier le résultat final de ces appels récursifs. En fait, l’ordinateur va automatiquement empiler chaque appel de fonctions afin de connaître l’ordre des appels, et avoir des informations au sujet des fonctions actives. C’est ce qu’on appelle la pile d’exécution.
Les piles d’exécution
L’ordinateur doit retenir le résultat de tous les calculs récursifs avant de finir sa boucle. Il utilise alors ce que nous appelons une « pile d’exécution » (en anglais, stack). Celle-ci est gérée automatiquement par le système.
Prenons par exemple le cas cette fonction main dans le labyrinthe :
Algorithme main()
Variable
joueur_position_x ← 0 : ENTIER
joueur_position_y ← 0 : ENTIER
arrivée_position_x ← 5 : ENTIER
arrivée_position_y ← 5 : ENTIER
clés[3] : TABLEAU CHAÎNE DE CARACTÈRES
Début
Tant Que joueur_position_x != arrivée_position_x ET joueur_position_y != arrivée_position_y ET clés.taille() != 3:
déplacement(joueur_position_x, joueur_position_y)
ramasser(clés, joueur_position_x, joueur_position_y)
Fin Tant Que
Fin
Lorsque la fonction main est appelée, on la place dans la pile d’exécution :
| main() |
et elle y est tant qu’elle est active, c’est-à-dire qu’elle n’est pas terminée.
Ensuite dans la fonction main , nous appelons une première fois la fonction déplacement dans la boucle Tant que , on l’ajoute ainsi dans la pile d’exécution, au-dessus de la fonction main .
| déplacement(joueur_position_x, joueur_position_y) main() |
Tout de suite après, la fonction déplacement se termine, donc on la déplie :
| main() |
Mais dans la ligne suivante, on appelle la fonction ramasser donc on l’empile. On a donc maintenant :
| ramasser(clés, joueur_position_x, joueur_position_y)main() |
Et la fonction ramasser , de la même manière, sera dépilée lorsqu’elle sera terminée, et ainsi de suite tant que la boucle est active. Lorsqu’elle se termine, la fonction main se termine aussi. Et donc on retire aussi la fonction main de la pile d’exécution. Quand la pile est vide, le programme est terminé !
La pile d’exécution peut aussi se noter « pile d’appels ».
Dans le cas d’un appel récursif, c’est exactement ce qui se passe !
Considérons la fonction récursive suivante :
Algorithme compteur(n)
Si n > 0 :
compteur(n - 1)
Fin Si
Afficher n
Fin
empile
Lorsque nous appelons la fonction compteur avec n=2 , nous avons la pile d’appels suivante :
| empile compteur(2) | empile compteur(1) | empile compteur(0) |
| compteur(2) | compteur(1)compteur(2) | compteur(0)compteur(1)compteur(2) |
Tant qu’il y a des appels récursifs de la fonction compteur , on les empile dans la pile d’exécution.
dépile
Lorsque la dernière fonction récursive est appelée, l’ordinateur « dépile » l’ensemble des fonctions présentes dans la pile d’exécution. Autrement dit, il va chercher dans la pile le dernier élément enregistré, et ainsi de suite jusqu’à arriver en bas de la pile. Bien pratique !
| dépile compteur(0) | dépile compteur(1) | dépile compteur(2) |
| compteur(0)compteur(1)compteur(2) | compteur(1)compteur(2) | |
| Affiche 0 | Affiche 1 | Affiche 2 |
À vous de jouer !

Contexte
Pour finaliser notre labyrinthe, nous souhaitons ajouter une dernière fonctionnalité. Nous allons créer des cases pièges, qui bloqueront le joueur pendant 10 secondes à chaque fois que le joueur passera dessus.
Consigne
Vous allez pour cela créer une fonction récursive qui bloquera le joueur pendant n secondes, et qui affichera un compte à rebours du temps restant pour être débloqué. Vous appellerez cette fonction freeze .
Considérez que la fonction attendre permet de mettre en pause le jeu pendant un certain nombre de secondes. Le nombre de secondes est passé en paramètre de la fonction.
Votre objectif :
- Définir une fonction
freezequi prend en paramètre le nombre n de secondes à bloquer. - Afficher le nombre de secondes restantes.
- Mettre en pause le jeu 1 seconde.
- Appeler récursivement la fonction
freeze. - Spécifier la condition d’arrêt de la fonction récursive.
Vérifiez votre travail
Voici le résultat à obtenir à l’issue de l’exercice :
Algorithme freeze(n)
Si n == 0 :
arrêter l’appel recursive
Fin Si
Afficher n
attendre(1)
freeze(n - 1)
Fin
En résumé
- Une fonction récursive est une fonction qui s’appelle elle-même pendant son exécution.
- Les étapes pour construire une fonction récursive :
- Décomposer le problème en un ou plusieurs sous-problèmes du même type. On résout les sous-problèmes par des appels récursifs.
- Les sous-problèmes doivent être de taille plus petite que le problème initial.
- Enfin, la décomposition doit en fin de compte conduire à un élémentaire qui, lui, n’est pas décomposé en sous-problèmes (c’est la condition d’arrêt).
- La pile d’exécution sert à enregistrer des informations au sujet des fonctions actives dans un programme informatique.
C’est bon, c’est promis, cette fois c’est vraiment terminé ! Bravo pour l’ensemble de votre travail tout au long du cours. Et je vous dis à tout de suite dans le dernier dernier quiz de ce cours pour valider vos connaissances. Je sais que vous adorez les quiz !